小数視力VS対数視力、対数視力の表記法

Last Updated on 2年 by 管理者

小数視力と対数視力の並び

• 小数視力とは、視角の逆数で表されます。
  • 例：視角１分＝1/1=小数視力1.0
  • 例：視角10分＝1/10=小数視力0.1
• 対数視力とは、10を底とした視角の対数で表されます。
  • 例：視角１分＝log1=logMAR0.0
  • 例：視角10分＝log10＝logMAR1.0

日本では小数視力が用いられております。但し、小数視力の並びは等間隔ではありません。

どういう事？って思いましたよね。

小数視力の並びは『0.1』の次は『0.2』・・・『0.9』の次は『1.0』となり数字的には等間隔ですが、倍率で考えますと一定ではありません。

小数視力が高くなる程、その倍率差は少なくなっていきます。

つまり、例えば、小数視力の『1.2』と『1.5』はそれほど変わらず、同じ0.3の違いでも『0.1』と『0.4』は大きく変わるという事です。

• 例えば
  • 小数視力『0.9』は『1.0』の
    • 0.9倍、差は0.1
  • 小数視力『0.1』は『0.2』の
    • 0.5倍、差は0.1

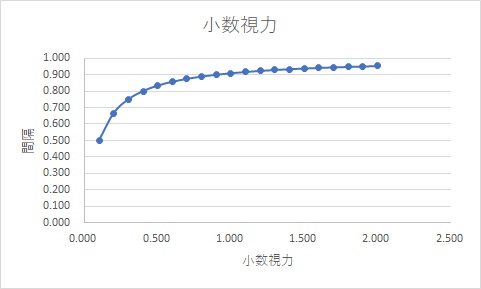
一方で、対数視力の並びは等間隔となります。

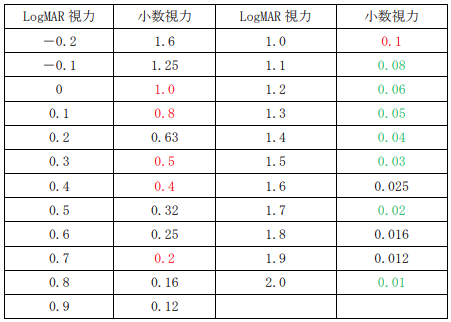
logMAR1.0=小数視力0.1、logMAR0.9=小数視力0.126、logMAR0.8=小数視力0.158・・・のような並びで視力表を作成すると等間隔な倍率となります。

• 例えば
  • logMAR0.9＝小数視力0.126は、logMAR1.0＝小数視力0.1の0.126倍
  • logMAR0.1=小数視力0.794は、logMAR0.2=小数視力0.631の0.126倍

つまり、視力表をlogMARで等間隔の並べ方をしますと、

小数視力でいう、2.512、1.995、1.585、1.259、1.000、0.794、0.631、0.501、0.398、0.316、0.251、0.200、0.158、0.126、0.100、0.079・・・のような視標の作りかたをすると等間隔になります。

小数視力で慣れてしまった我々には、今更、対数視力の表記にしますと、誤解や混乱が生じます。デメリットの方が高いです。

視力検査の目的

『視力検査』は、いろいろな目的で行われております。

例えば、免許更新などの適性検査、目の健康状態の診断、臨床検査、眼鏡の処方度数決定の参考にしたり・・・

と、視力検査が実施されている分野はすごく広いです。

その『視力』というのは、被検者の健康状態などでも変化はしますが、毎回大きく違ったり、信頼できないものであっては困ってしまいますよね。

では、本当に『Landolt環』で良いのでしょうか？

例えば、乱視が無い人でも、特定の方向で見え方は変わるという報告がいくつもあります。

『照明の輝度』、『配列』、『寸法の許容差』、『正解率とその視力』は？

独自の『視標』を作れたら面白いな・・・と少し考えましたが、

『Landolt環』以上に、バランスがとれた優れた視標を考案するのは難しいなぁ・・・とすぐに気付きました。

Landolt環の歴史

SnellenおよびGiraud Teulonが、最小視角１分を標準とする方式で視標を発表しました。

それ以来、視角１分を視力の単位として広く認められるようになり、視標の寸法を決める基礎は『Snellenの１分角説』となっております。

1888年に、Landoltが１分角説による『Landolt環』を発表し、

1909年には、国際眼科学会にて、視力検査の『国際的標準視標』に採用されました。

視力表に求められる条件

• 検査の正確性
• 検査の簡便迅速
• 推量で正答できない
• 検査に智能を要しない
• 視標が小型で簡単構造

以上の事をより多く満たせる視標が良いと考えます。

そう考えますと、Landolt環は、結構優秀ですよね。

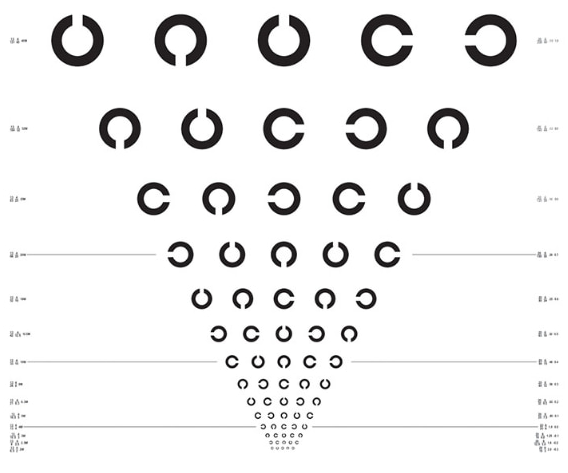
他にも以下に示すような、１分角説による視標があります。

左上から、Landolt環、Ferree Rand環、Snellen鉤、Bostrom鉤、ローマ字視標、右図は市松模様視標です。

log MARでの視力表記

• 【例１】
• log MAR=0（小数視力1.0）の列を全て正しく答えた場合
  • 視力は 0.0＋0.00=0.00
• log MAR=0の列を１つ間違えた場合
  • 視力は0.0＋(0.02×1)=0.02
• log MAR=0の列を2 つ間違えた場合
  • 視力は0.0＋(0.02×2)=0.04
• log MAR=0の列を３つ間違えた場合は0.06
• log MAR=0の列を4つ間違えた場合は0.08
• log MAR=0 の列を全て間違えた場合
  • 0.0+(0.02×5)=0.1となり、１段階大きい視標の列が示されます。

• 【例２】
• log MAR=0.1（小数視力0.8）の列で２つ間違えた場合
  • 視力は、0.1＋(0.02×2)=0.14

• 【例３】
• log MAR=0の列を全て正しく答え、次の列の視標２つ正しい場合
  • その数に0.02を掛け、0から引きます
  • 0.0–(2×0.02)=－0.04

• 【例４】
• log MAR=−0.1の列の全て正しく答え、次の列の視標１つ正しい場合
  • －0.1－(0.02×1)=－0.12