収差の解説

Last Updated on 2年 by 管理者

収差の実例

レンズを傾けて物体を見た時、像がボヤケたり乱視のように伸びて見えます。

格子状の物を見た時には樽型に歪んで見えたりもします。

強度数レンズの周辺で光源を見た時には光が虹色に見えます。

これらは全て、収差といわれる現象による影響です。

収差（aberration）の定義

JIS規格では、収差の定義を『光学系によって結像する場合、像の理想像からの幾何光学的なずれ』としています。

つまりは、

『ある１点から出た光束は、レンズなどにより再度１点に集まる』というのは数学的近似（例：sinθ≒θ）がなされている理想であり、実際は『完全に１点に集まる』という事は通常ありません。

不完全な結像の為、ぼやけて見えたり、歪んで見えます。この理想的な写像からのズレを収差といいます。

これは、大別して光学系の分散による『色収差』と、単色光を用いても生じる『単色光収差』の２つがあります。

因みに、sin θを級数展開（Maclaurin展開）しますと、
『sin θ=θ−θ³/3!+θ⁵/5!−θ⁷/7!+θ⁹/9!−・・・』となります。

入射角のθが大きくなりますと、近似する事ができなくなります。

そこで、第２項までの『sinθ=θ−θ³/3!』について考慮した場合に５つの収差が表れます。

この５つの収差を、『Seidel（ザイデル）の５収差』といいます。

ザイデルの５収差はθ³までですので、『３次収差』ともいいます。

θ⁵より先・・・の収差を、『５次収差』や『７次収差』といい、総称して『高次収差』といいます。

収差の種類

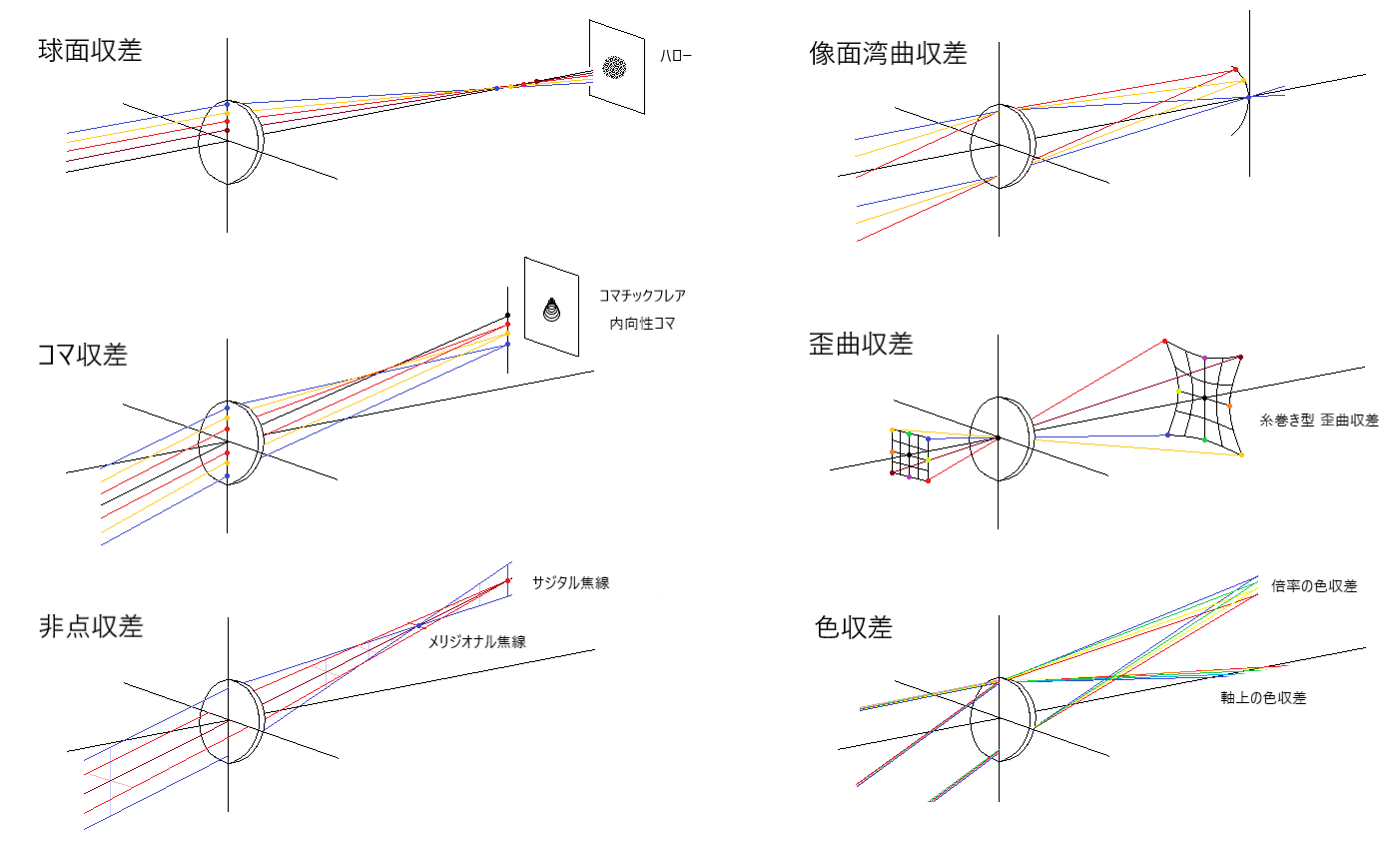
球面収差、歪曲（わいきょく）収差、コマ収差、非点収差、像面湾曲収差、高次収差、色収差などがあります。

• 収差の種類
  • ザイデルの5収差
    • 球面収差（spherical aberration）
    • コマ収差（comatic aberration）
    • 非点収差（astigmatism）
    • 像面湾曲収差（curvature of field）
    • 歪曲（わいきょく）収差（ディストーション：distortion）
      • 樽型歪曲（barrel distortion）
      • 糸巻型歪曲（pincushion distortion）
  • 高次収差
  • 色収差
    • 軸上の色収差、又は縦方向の色収差
    • 倍率の色収差、又は横方向の色収差

収差にも種類はいくつかありますが、実際の眼鏡レンズで問題になる収差は、『非点収差』と『歪曲収差』、『色収差』です。

その理由としては、

瞳孔径がφ3～4mmとしますと、『球面収差』や『コマ収差』はほとんど無視しても良い程のものになります。

網膜がほぼ球面である事から、『像面湾曲収差』も無視しても良い程度となるからです。

筆者が20代前半の新卒で、東京表参道の眼鏡店に入社したばかりの若かりし日の体験談ですが、

眼鏡を買いにいらしたカップルの男性が『この眼鏡に収差が無いレンズで！』と購入前の商品であるフレームを乱雑にポンと投げてきました。

その態度に少しイラついた私は、『収差が全く無いレンズはありませんが、収差を抑えたレンズならございます。非点収差を抑えたレンズであれば〇〇、色収差が少ないレンズであれば〇〇です。何収差ですか？』と聞き返してしまいました。

そもそも、この男性から『収差』という言葉が出るとは・・・。

案の定、『収差は収差だよ。』と言われ、『申し訳ありません。（大人気なく難しい言葉を使い、聞き返した事に対して）』っと普通にスルーしました。

聞き返した理由は、眼鏡作製した後で、『収差がある。収差が無いレンズでって言ったよな・・』とクレームになるのが嫌だったからなのですが・・。

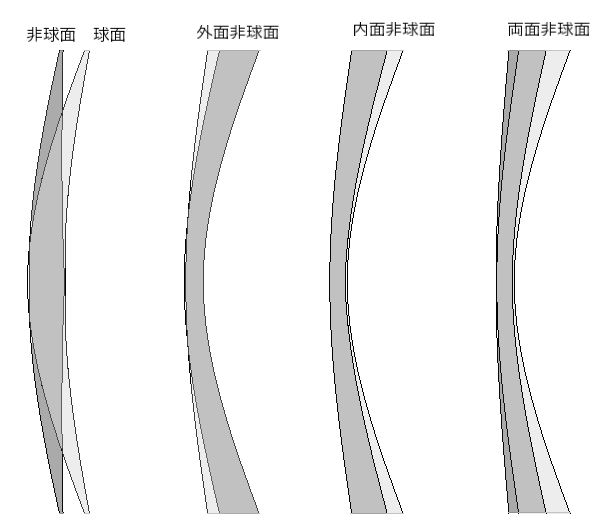
ざっくりと、非点収差を抑える為には、非球面設計のレンズ（片面非球面（AS）よりも両面非球面（DAS）の方が良い）です。色収差を抑える為には、アッベ数が高いレンズ（比較的、低屈折率の方がアッベ数が高い）が色収差が少ないです。

球面収差

球面収差とは、軸外の光線が必要以上に屈折する以下のような収差です。

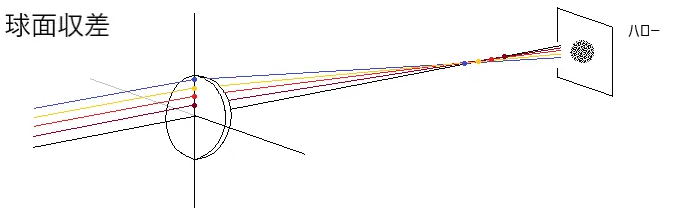
球面収差には、縦方向と横方向があります。

軸上の差を『縦方向球面収差（longitudinal spherical aberration : LA）』といい、近軸像面における差を『横方向球面収差（lateral spherical aberration : TA）』といい、図に示しますと以下のようになります。

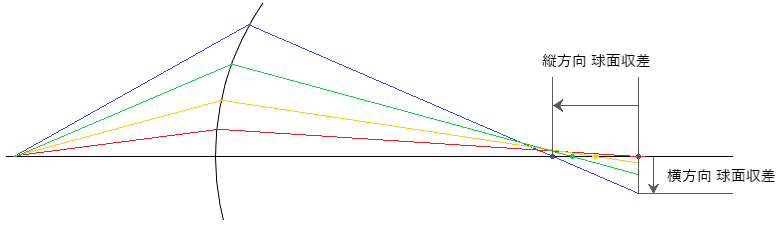
縦方向球面収差は、入射角が大きくなるにつれ放物線状に大きくなります。

以下のような球面収差曲線は、縦軸に近いレンズほど球面収差が少なくなります。

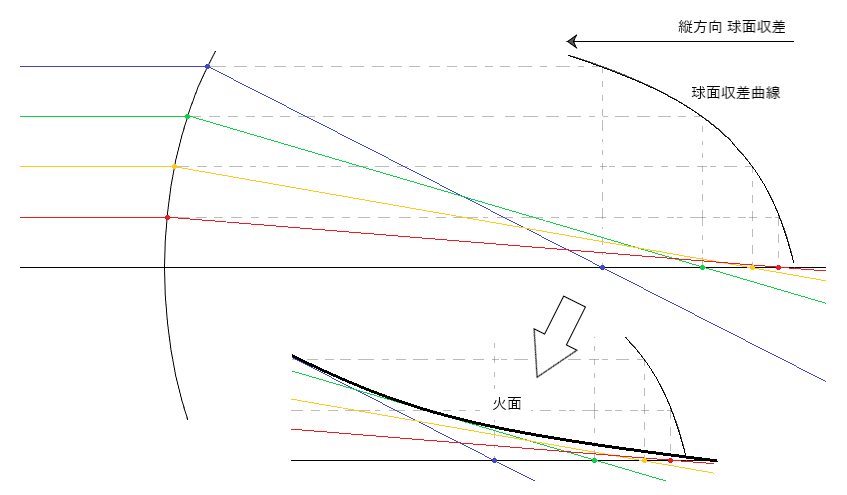
レンズ後方における光束の包絡面は円錐ではなく、上図のような曲面になり、これを火面（かめん）（caustic surface ）といいます。

球面収差の補正

眼鏡レンズの場合には、光束が少ない範囲である為に影響が少なく、原則としては設計時に考慮はしません。

但し、収差を抑える為の原理を知る事は必要なことと考えます。

球面収差が生じる原因は、レンズの周辺部になるほどに屈折力が大きくなる事です。

球面収差を抑える為の方法をいくつか挙げます。

例えば、非球面設計レンズのように周辺部にいくにつれ曲率半径を小さくする事です。

他には、レンズ周辺部の屈折率を、中心部よりも徐々に小さくする事です。

また、合成レンズにする事です。一方のレンズで生じた球面収差を他方レンズの逆符号で打ち消すように張り合わせる事です。

コマ収差

ある光学系に対し、球面収差が除去された場合には、軸上物点の結像は完全となり鮮鋭な像を作ります。

しかし、物点が軸上から離れるとコマ（coma）という彗星（comet）の形に似た収差が発生します。

球面収差を除去した、コマ収差のみの図を以下に示します。

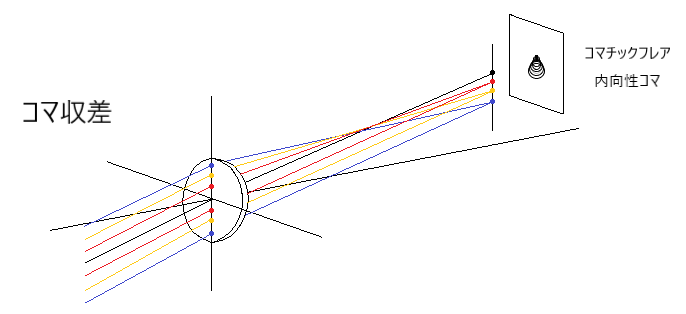
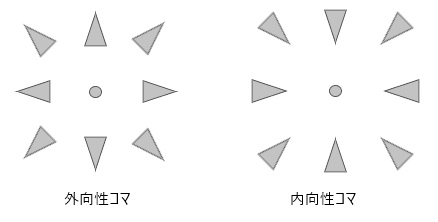
レンズの端を通る光線よりも、レンズ内側を通る光線の横倍率が大きい場合には負のコマ（外向性コマ）が発生します。

レンズ中心部を通る光束が最も明るく、周辺部になるにつれ急激に明るさが減少します。

逆にレンズ内側を通る光線の横倍率が小さい場合には正のコマ（内方性コマ）が発生します。

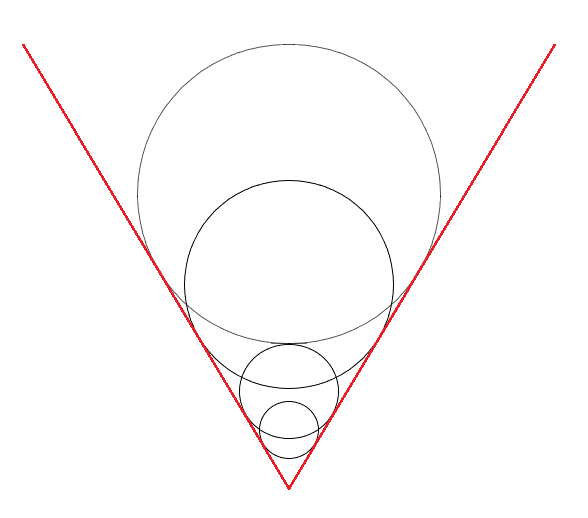
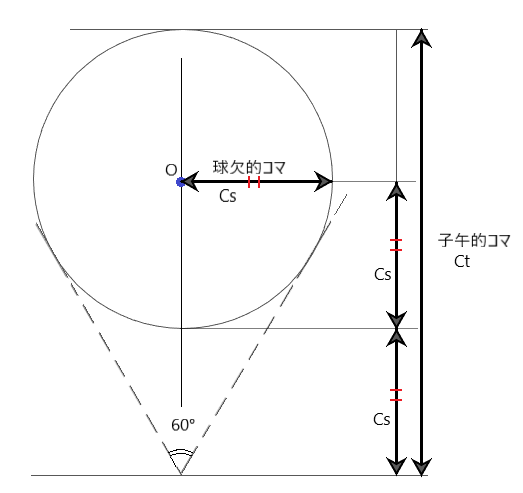
以下のようなCsを球欠的コマ、Ctを子午的コマといい、Ct=３Csという関係が成り立ちます。

瞳孔径がφ3～4mmであるため、『球面収差』と同様に、『コマ収差』でもあまり問題とはなりません。

非点収差

球面収差とコマ収差の２つが除去されたとしても、物点がかなり軸から離れると結像が非点的（astigmatic）となります。

球欠的光束と子午的光束は、点ではなく互いに直交する直線となります。

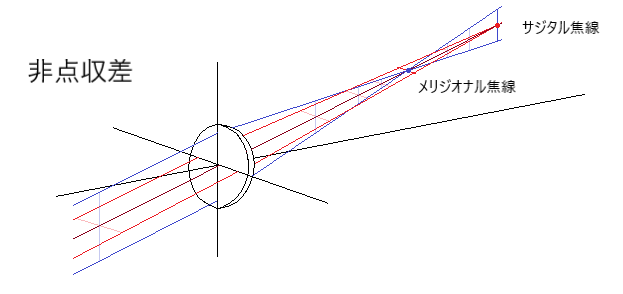
非点収差は、眼鏡レンズで問題になる収差となります。

像面湾曲収差

仮に、球面収差やコマ収差、非点収差が完全に除去されたとしても、まだ完全な結像とはなりません。

点に完全に結像されたとしても、それぞれの点の像が平面ではなく、以下のような曲面上に結像されてしまうからです。

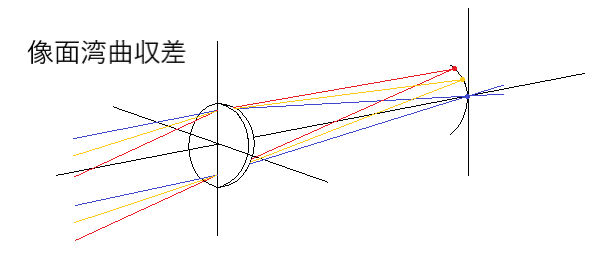
網膜の形状がほぼ球面である事から、『像面湾曲収差』は眼鏡レンズではあまり問題とはなりません。

歪曲（わいきょく）収差

JIS規格では、歪曲収差をディストーション（distortion）といいます。

『横倍率画像の大きさにより異なる収差』と定義されております。

もし仮に、球面収差、コマ収差、非点収差、像面湾曲収差の４つの収差が全て除去された場合でも結像は完全にはなりません。

平らな像面上で鮮鋭に結像したとしても、元の像と相似ではない像を作るような収差があるからです。

これを歪曲収差（ディストーション）といいます。

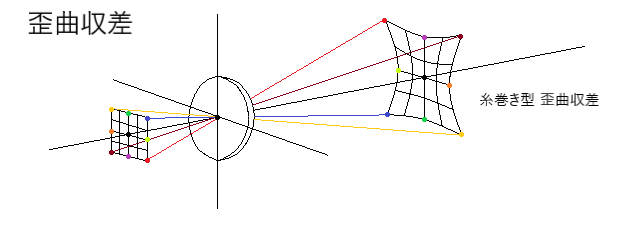
歪曲収差には、糸巻型、樽型、陣笠（じんがさ）型があり、網状の物体が以下のような歪みが生じます。

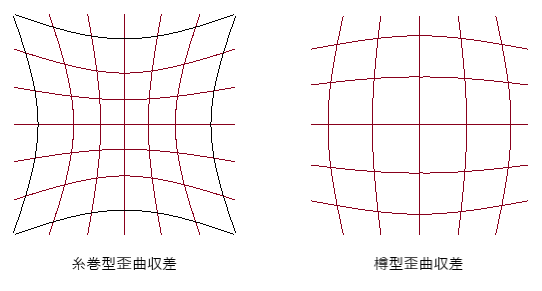
一般的には、凸レンズは糸巻型になり、凹レンズは樽型に歪みます。

周辺部になるにつれ倍率が大きくなる場合には糸巻型になり、逆に倍率が小さくなる場合には樽型に歪みます。

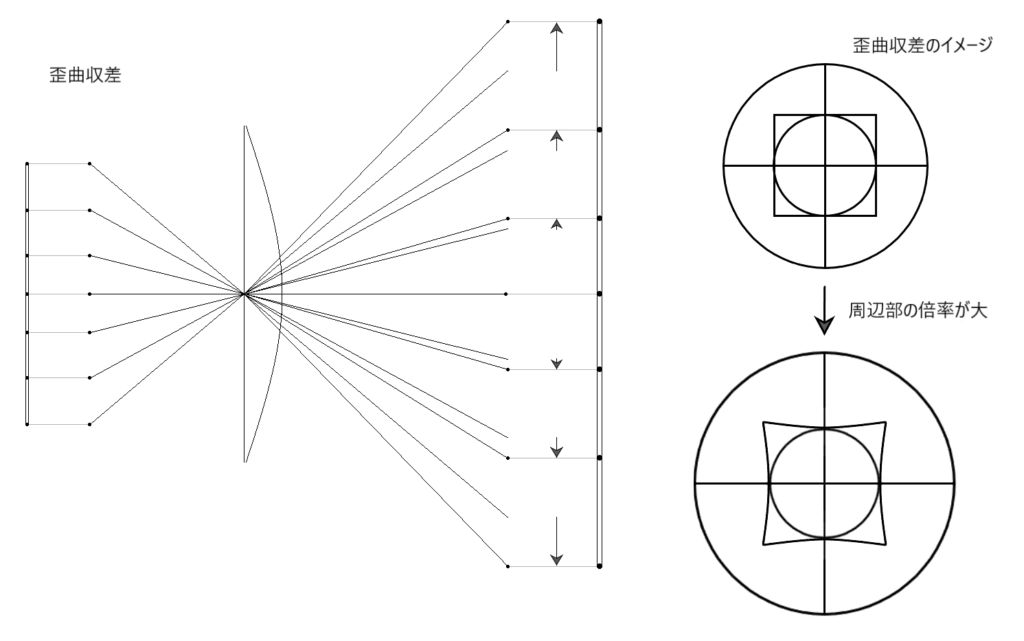
単レンズでは、実用上な問題はありませんが、他の収差を補正する為に他のレンズや絞りを組み合わせると歪曲収差が大きくなります。

歪曲収差は、眼鏡レンズで問題になる収差となります。

高次収差

ある単レンズに対し、３次収差論により得られる球面収差と、厳密な光線追跡論法により得られる球面収差を比較しますと、入射高が小さければ一致しますが、光線の入射点が光軸から離れるにつれて両者は一致しなくなります。

これは、sinθのマクローリン展開である『sinθ=θ−θ³/3!+θ⁵/5!−θ⁷/7!+θ⁹/9!−・・・』の３次の項まででは不十分であるためです。

５次の項までを考慮しますと光線追跡論法により得られる球面収差にかなり近づきます。

色収差

Newtonさんは、太陽からの白色光をプリズムに当て、虹色に分解される事を発見したとされております。

レンズは、プリズムを多数集めたものと考える事ができます。

下図のように、軸上にできる像位置の差を『縦方向色収差（軸上の色収差）』といい、軸に垂直な方向の差を『横方向色収差（倍率の色収差）』といいます。

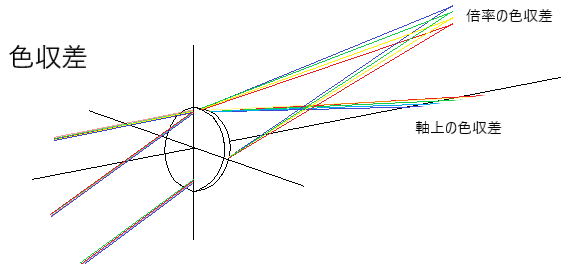
色収差は、強度数のレンズでは問題となる収差となります。

色収差が少ないレンズは、アッベ数（Abbe数）が高いレンズであり、比較的屈折率が低いレンズです。