Last Updated on 1年 ago by 管理者
随時更新しております。
( ..)φ メモ
1.屈折率1.0の媒質から屈折率1.5の媒質に入射角30°で入射した光線の屈折角は約何度?
【解説】
屈折の法則(スネル・デカルトの法則):「n1 sinθ1=n2 sinθ2」から
1.0×sin30°=1.5×sinθ2
1.0×1/2=1.5×sinθ2
sinθ2=0.5/1.5≒0.33
θ2=sin-10.33≒19.47°
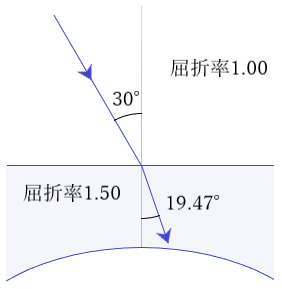
2.屈折率1.5の媒質から光線が空気中に入射するときの臨界角は?
【解説】
屈折の法則(スネル・デカルトの法則):「n1/n2=sinθ2/sinθ1」から
臨界角を求めるには、θ2=90°として
1.5/1.0=1/sinθ1
sinθ1=1.0/1.5
θ1=sin-1(1.0/1.5)≒41.8103°
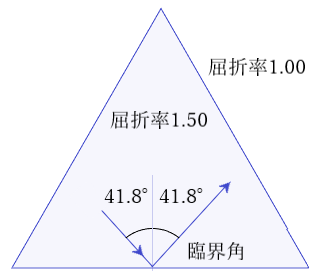
つまり、41.81°以上の入射角では屈折せずに全反射します。また、全反射は屈折率が高い媒質から低い媒質へ入射する場合に起こります。
例えば、大気中(屈折率1.00)から水中(屈折率1.33)への入射では全反射が起こりませんが、水中からは全反射が起こります(水の臨界角は約48.8°)。
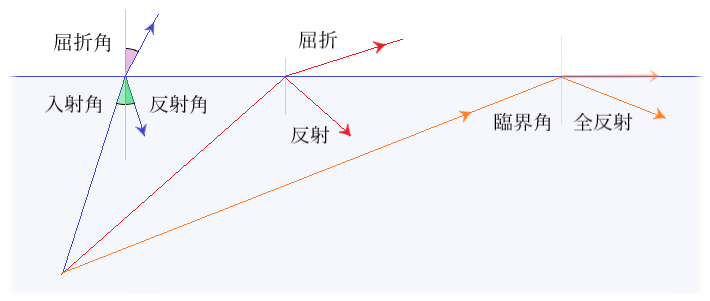
全反射はエネルギー損失がないため、光路の方向を変える方法として鏡を用いるよりも全反射プリズムの方が優れています。
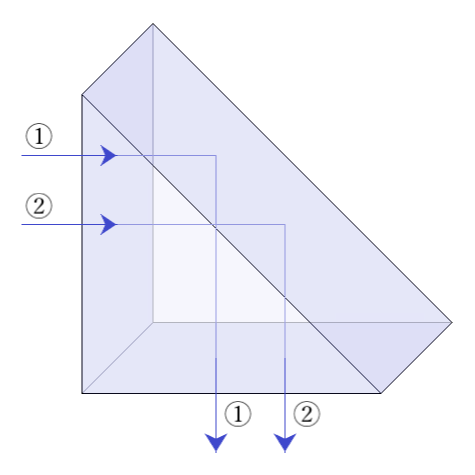
3.1m離れた平面鏡の前に立ち、鏡に映る自分のつま先を見たときの像は鏡の裏側何メートルの距離に像が見えますか?
【解説】
平面鏡を境に、物体と面対称の位置に虚像ができます。
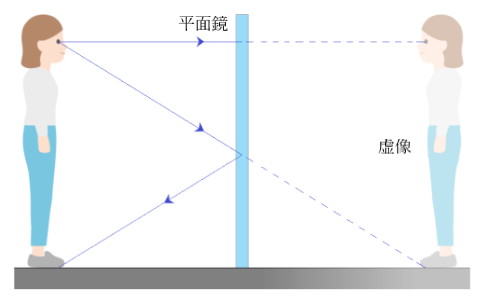
累進眼鏡での近用フィッティングで用いられる「ミラー法」の根拠となる原理です。
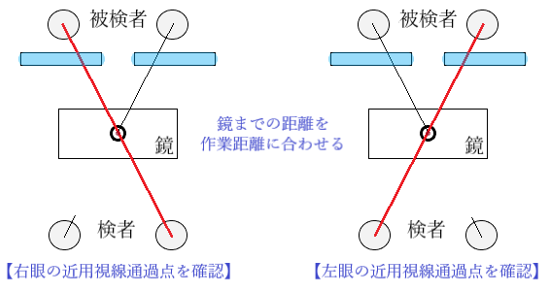
- ミラー法では、近用FPが近用視線通過点と一致しているかどうかを確認できますが、正直〇が小さくて見づらい、、、。
4.凸面鏡に映る像は実像?虚像?正立?倒立?
【解説】
凸面鏡では、物体の距離に関係なく常に小さい正立虚像ができます。これは、道路のカーブミラーや車のサイドミラーなどで使用され、倒立像になると混乱して事故になってしまいますね。
一般的に焦点距離は曲率半径の半分の位置にあります。
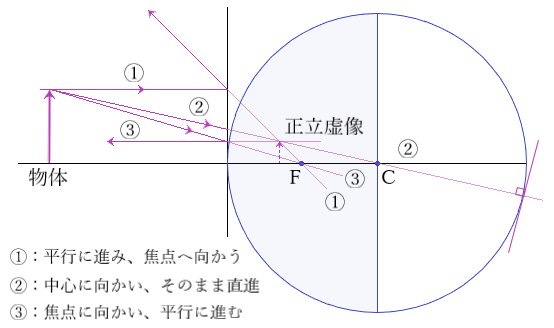
凹面鏡による実像と虚像を求める作図をしますと以下のようになります。物体が凹面鏡の焦点よりも鏡に近い位置では大きな正立虚像ができます。
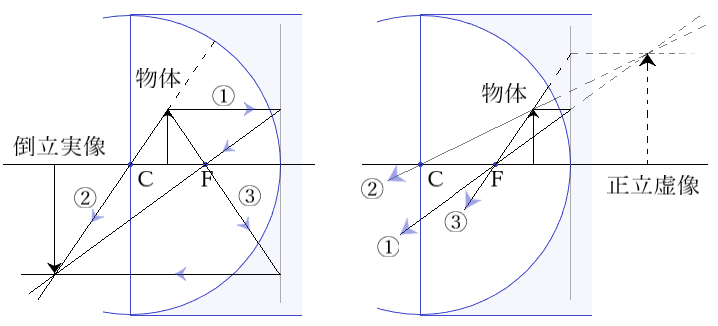
実像と虚像の違いは、例えばその位置にスクリーンを置いたときに映せるかどうかです。映るのが実像で虚像は映りません。ヒトが虚像を見ることができるのは、網膜というスクリーンに実像が映るからです。
5.オートレフケラトメータにて観測している像は、4つのプルキンエ・サンソン像のどれ?
【解説】
角膜表面からの反射光がつくるマイヤーの虚像は第Ⅰ像です。
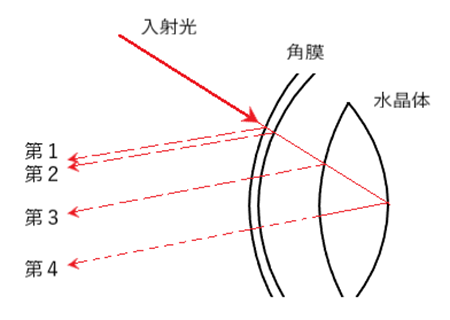
例えば、凸面鏡では常に小さな「正立虚像」がつくられ、凹面鏡では焦点距離よりも離れた位置に物体がある場合では「倒立実像」がつくられます。
- Purkinje-Sanson像
- 第Ⅰ像:角膜前面からの反射・・正立虚像
- 角膜反射像とも呼ばれ、きわめて明るい。第Ⅱ像~第Ⅳ像は暗い。
- 角膜表面の曲率半径が約7.8mmとすると焦点位置7.8/2=3.9mm付近に虚像がつくられ、入射瞳が約3mmであるので見かけの瞳孔(入射瞳)の後方約1mmに角膜反射像ができているといえる。
- 第Ⅱ像:角膜後面からの反射・・正立虚像
- 第Ⅲ像:水晶体前面からの反射・・大きい正立虚像
- 調節により大きさと結像位置が変化する。
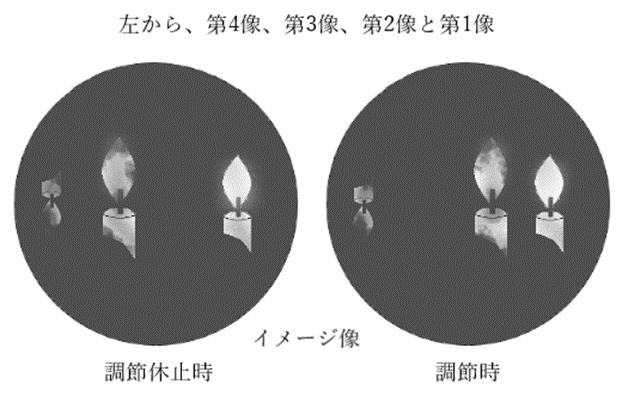
- 第Ⅳ像:水晶体後面からの反射・・小さい倒立実像
- 調節により大きさと結像位置が少しだけ変化する。
- 第Ⅰ像:角膜前面からの反射・・正立虚像
6.2Δのプリズムが、5m先でおこる偏位は何cm?
【解説】
1m先で1cmの偏位がおこるプリズムを1Δとします。2Δのプリズムは1m先では2cmの偏位がおこり、5m先では10cmの偏位がおこります。
7.球面度数 S+5.00Dのレンズが光学中心から10mm離れた距離でのプリズム量は?
【解説】
プレンティスの近似式:「PΔ=h[cm]×D[D]」から、
P[Δ]=1[cm]×5.00[D]=5Δ
球面レンズ S+5.00の焦点距離はf=1/5.00=0.2[m]ですので、レンズ光学中心から1cmずれた位置を通る平行光線が焦点を通るように作図をしますと、1m先での偏位は5cmとなり5Δとなります。
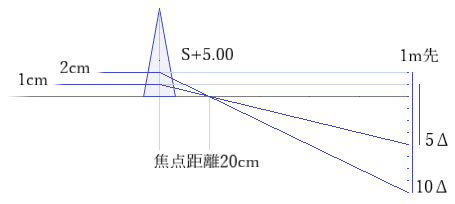
レンズ光学中心から1cmずれは5Δ、2cmずれは10Δとなり、プレンティスの公式:「P=h×D」と一致します。
8.+0.5Dの凸レンズにて、5m先の物体がつくる像の位置は?
【解説】
ガウスの結像公式:「1/s’−1/s=D(物体距離:s、像距離:s’)」から、
1/s’−1/(−5)=0.5
1/s’+0.2=0.5
s’≒3.33[m]
この時、平行光線が右方向に進むようにイメージします。物体距離はレンズの右側になりますので符号はマイナスです。s=−5として計算しますと(s=5としないように注意!)、s’の符号がプラスですのでレンズの右側に像がつくられます。
光線が右方向に進むように作図しますと以下のようになります。↓
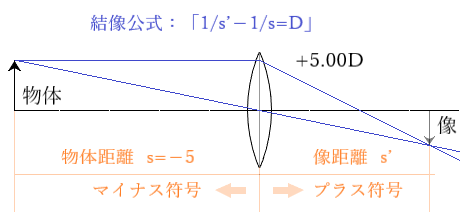
計算で求めた3.33mの位置にしっかり倒立像が描けます。
9.入射バージェンス:U、レンズ屈折力:D、射出バージェンス:V としたときの基本式は?
【解説】
vergenceとは、ある点から出た(へ向かう)光線の発散や収束の程度を表します。入射でも射出でも発散光線束のバージェンスは負となります。D>0は凸レンズ、D<0は凹レンズです。
入射バージェンス U=0、U<0、U>0 の図をそれぞれ以下に示します。
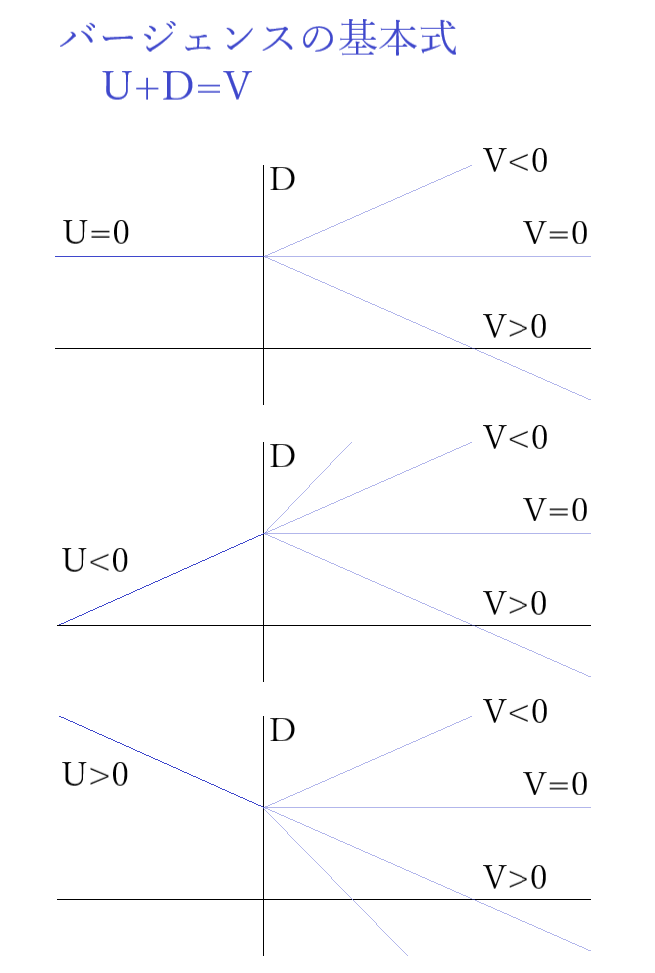
例えば、「U>0、D>0」のときは、必ず「V>0」となります。また、「U<0、D<0」のときは、必ず「V<0」となります。
10.大気中(屈折率1.0)に置かれた厚いレンズの場合、物体主点から物体焦点までの距離f、像主点から像焦点までの距離f’、物体距離s、像距離s’を公式で表すと?
【解説】
レンズ前面側の屈折率nと後面側の屈折率n‘’ が大気に接している場合には、「n=n’’=1」として表せますので、「 n’’/s’ − n/s = −n/f = n’’/f’ 」に当てはめると、「1/s’−1/s=−1/f=1/f’」になります。
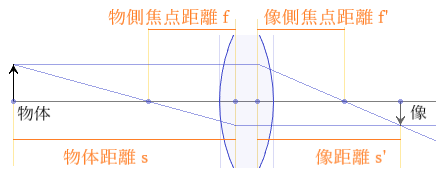
2枚の薄いレンズを離して置くときの合成屈折力は、厚いレンズと同様に扱えます。
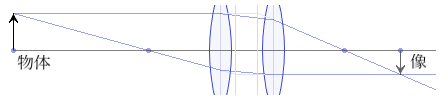
11.「光がある一点から他の一点へ進むとき、時間が最も少なくて済む道筋を通る」という原理を何という?
【解説】
光の直進、反射の法則、屈折の法則などは、フェルマーの原理から導かれます。
光は最短の時間で進むということで、「時間=距離÷速さ」から、A座標(0,a)から、O座標(x,0)を通り、B座標(b,d)へと向かう時間を求めてみます。
本当に、A座標➝B座標の最短距離よりも、O座標を経由した方が早いのかを検証していきます。
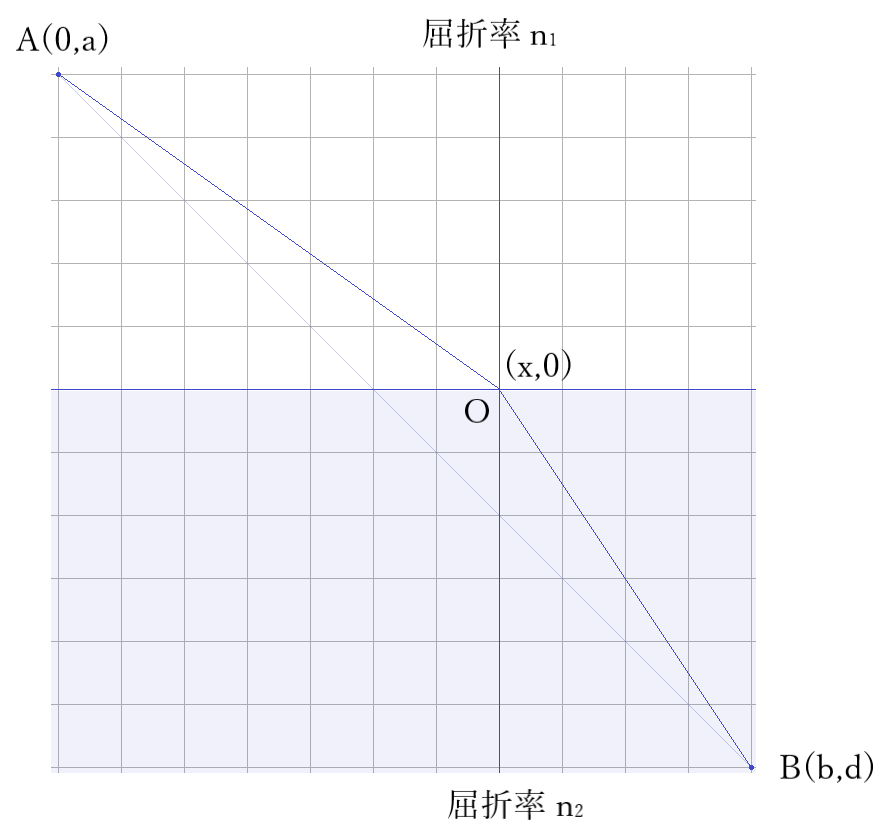
A座標➝O座標までの時間と、O座標➝B座標までの時間を足し合わせ、
「(a2+x2)1/2÷v1+((b-x)2+d2)1/2÷v2」 となります。
物質の屈折率とは、「屈折率n=真空中での光速c÷物質中での光速v」で表されますので、
「(a2+x2)1/2×(n1/c)+((b-x)2+d2)1/2×(n2/c)」 が最小時間となるようにA点➝O点➝B点へ進みます。
例えば、A(0,5)、B(11,-6)、n1=1.0、n2=1.5とした場合、
O座標のxの値は、
(52+x2)1/2×(1.0/c)+((11-x)2+(-6)2)1/2×(1.5/c)
=1/c{(25+x2)1/2+1.5((11-x)2+36)1/2} となります。
xが最小となる値を求めますと、約7.1となります。
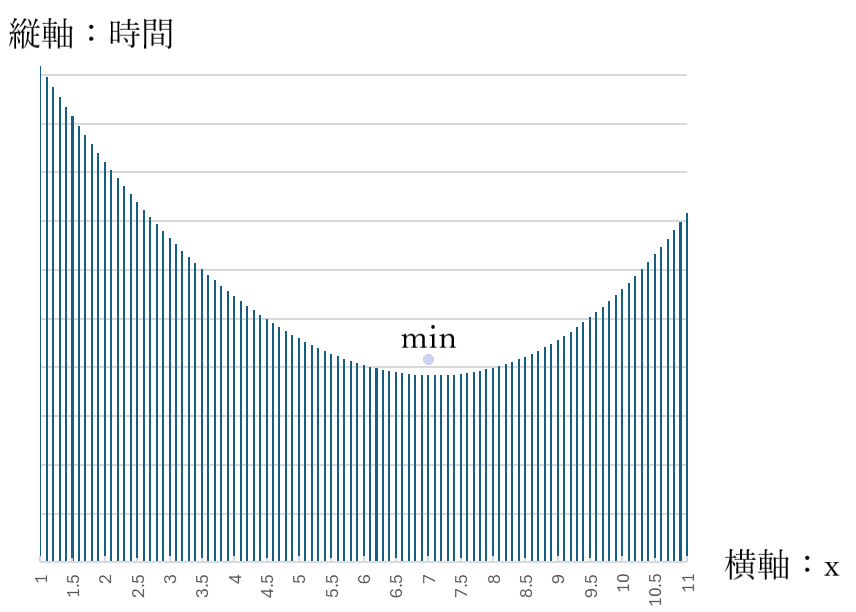
A座標➝B座標の最短距離の場合x=5よりも、O座標を経由したx≒7の方が時間が短いことがわかりました。
因みに、入射角 θとしてsinθ=x/(a2+x2)1/2、屈折角 θ’としてsinθ’=(b-x)/((b-x)2+d2)1/2から、sinθ/v1=sinθ’/v2が求められ、n1=c/v1、n2=c/v2を当てはめると、「Snellの法則:n1sinθ=n2sinθ’」が導き出されます。
12.薄いレンズを大気中から水中に入れた時の焦点距離はどう変化する?
【解説】
レンズの屈折力は、レンズとそのレンズに触れる媒質の屈折率の差に影響します。屈折率は、n大気=1 ➝ n水中=1.33 へ変化し大きくなることで、レンズとの屈折率の差は小さくなります。その分、屈折力も弱くなり、焦点距離fは長くなります。凹レンズ、凸レンズでも一緒でfは大きくなります。
- レンズが大気中にある場合 ↓[薄いレンズではレンズの厚み t=0とします。]
- レンズ前面の屈折力 D1=(nレンズ−n大気)/r1
- レンズ後面の屈折力 D2=(n大気−nレンズ)/r2
- レンズの屈折力 D=D1+D2−t/nレンズ (D1+D2)
上記の式からも、n大気=1 ➝ n水中=1.33へ値が大きくなる場合、D1、D2が小さくなりDも小さくなることがわかります。
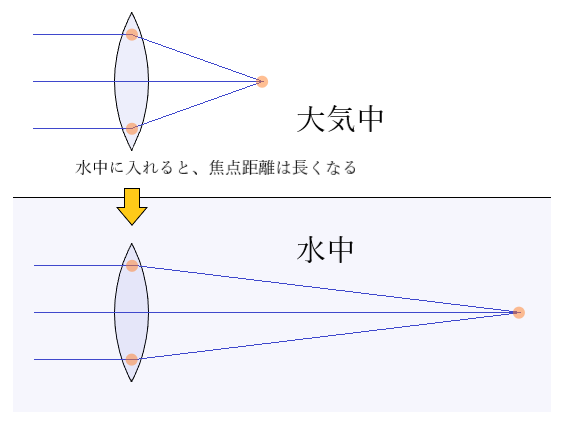
例えば、レンズ屈折率1.50、曲率半径 r1=1m、r2=−1mの凸レンズで計算しますと、D大気>D水中になります。
- D1大気=(1.50-1.00)/1=0.50
- D2大気=(1.00-1.50)/(−1)=0.50
- D大気=0.50+0.50=1.00
- D1水中=(1.50-1.33)/1=0.17
- D2水中=(1.33-1.50)/(−1)=0.17
- D水中=0.17+0.17=0.34
13.焦点距離2mの凸レンズと焦点距離−50cmの凹レンズを貼り合わせた合成レンズの焦点距離は?
【解説】
公式:D=D1+D2=1/f1+1/f2=1/f
凸レンズの屈折力はD1=1/2=+0.5D、凹レンズの屈折力D2=1/(−0.5)=−2.0Dです。重ね合わせたレンズの屈折力は D=D1+D2=−1.50Dです。
よって、求めたい焦点距離は f=1/(−1.50)≒−0.67m です。
14.前面の曲率半径が+10.00mm、後面の曲率半径が−6.00mmのレンズは凸レンズ?凹レンズ?
【解説】
レンズ前面の曲率半径がプラス符号であることから前面は凸、レンズ後面の曲率半径はマイナス符号ですが後面から見ると凸です。
曲率半径の値 |r1|>|r2|から、前面カーブの方が浅く緩やかな凸レンズとなります。
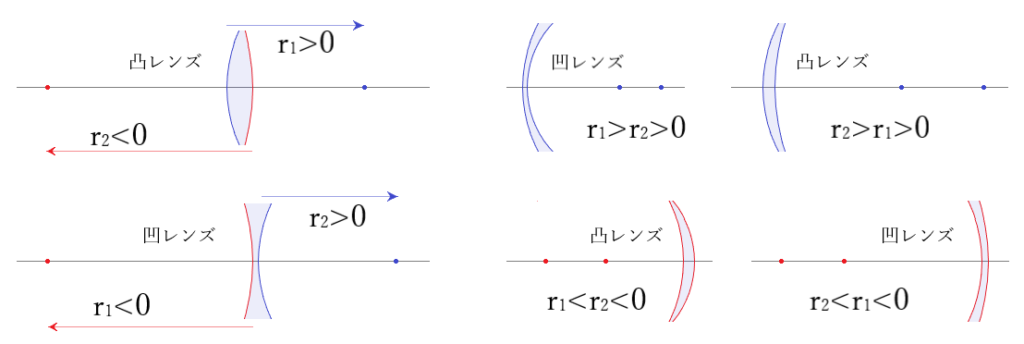
因みに、前面曲率半径 r1=10.00mm、後面曲率半径 r2=-6.00mmは水晶体(無調節状態)の曲率半径です。
調節時には主に前方に膨らみます、、、ということは、前面の曲率半径r1は調節により値が小さくなります。
15.屈折率1.5の素材でできた薄いレンズの前面が曲率半径25cm、後面が曲率半径10cmのレンズの屈折力は?
【解説】
薄いレンズの結像式(大気中 n=1.00):D=D1+D2=(n-1.0)/r1+(1.0-n)/r2
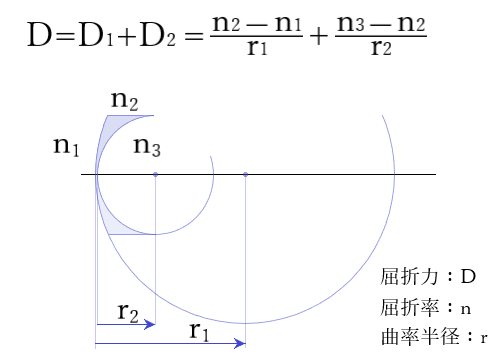
(1.5−1.0)/0.25+(1.0−1.5)/0.10=0.5/0.25−0.5/0.1=+2.0−5.0=−3.00[D]
別解) D=(n-1.0)(1/r1-1/r2)=(1.5-1.0)(1/0.25-1/0.1)=0.5×(4-10)=-3.00[D]
16.眼鏡レンズで問題となる収差は?
【解説】
- ザイデルの5収差:
- 球面収差・・瞳孔径がφ3~4mmであるため無視できる。
- コマ収差・・瞳孔径がφ3~4mmであるため無視できる。
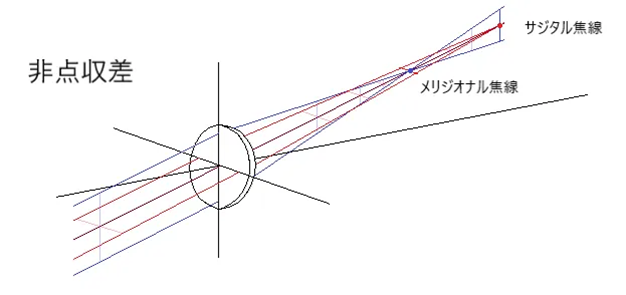
- 非点収差・・軸からかなり離れると結像が非点的(astigmatic)となる。
- 像面湾曲収差・・網膜がほぼ球面であるため無視できる。
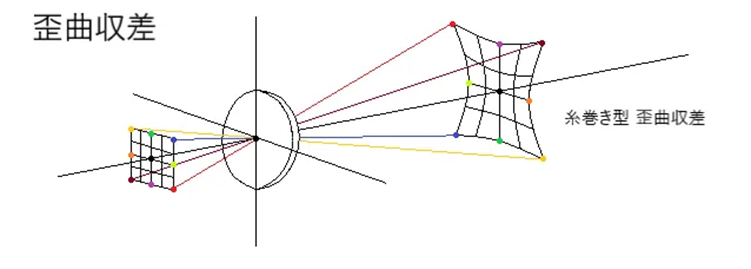
- ディストーション(歪曲収差)・・横倍率画像のように異なる収差。球面収差、コマ収差、非点収差、湾曲収差が除去されても完全な結像とはならない。
17.虹彩は何絞りの役割を担う?
【解説】
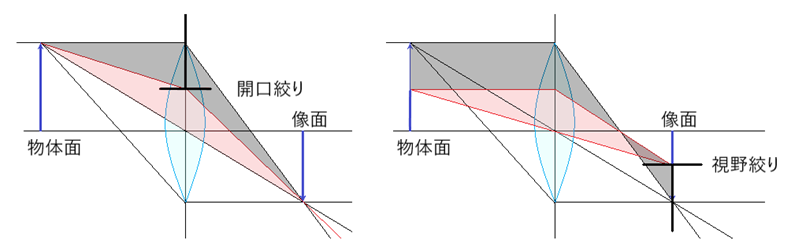
- 開口絞り・・瞳孔など、光量を制限する機構。像の明るさを決める。
- 視野絞り・・眼瞼など、視野を制限する機構。見える範囲を決める。
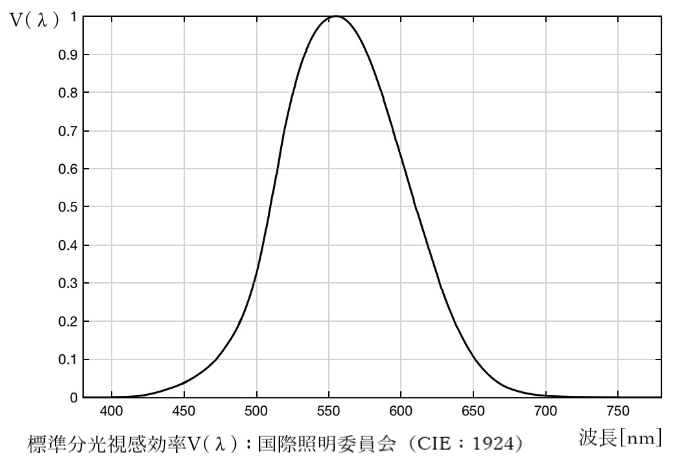
18.波長555nmの分光視感効率(比視感度)を1とし、その範囲はおよそ380~780nmですが、その両端の分光視感効率も1となる?
【解説】
分光視感効率とは、可視光(目に入って視感覚を起こすことができる放射)の境界となる波長範囲の中で最も明るく感じる黄緑色(555nm)を1とし、他の波長が相対的にどの程度に明るく感じるかを表した値です。
個人差もあり、照明環境にもよりますが、波長555nmの比視感度を1として両端ではほぼゼロです。可視光線の波長領域が見える範囲だとはいえ、全てが同様に明るく感じるわけではありません。
19.水面に垂直入射した光の反射率は何%?
【解説】
- 垂直入射の反射率:R=[(n1-n2)/(n1+n2)]2×100
- 入射側の屈折率n1、屈折側をn2とする。
大気と水の屈折率をそれぞれ、n空気=1.00、n水=1.33として計算しますと、
R水面=[(1.33-1.00)/(1.33+1.00)]2×100≒2.01% となります。
例えば、ノンコートレンズ(屈折率1.5)の表面反射は、((1.5-1.0)/(1.5+1.0))2×100≒4.0%として計算できます。レンズ両面では約8%です。この反射はゴーストやチラつきの原因になります。
レンズの屈折率が1.67の表面反射は6.3%、屈折率が1.76では7.6%の表面反射として計算できます。このように、屈折率が高いほど反射率も高くなります。
垂直に入射しない場合(入射角≠0)では、入射角θiで反射率Rは変化し、p偏光とs偏光で反射率RPとRSはそれぞれ変化します。入射面にparallel(平行)に振動するRPはゼロとなる角度があり、RP=0となる角度θBを「ブリュースター角」といいます。
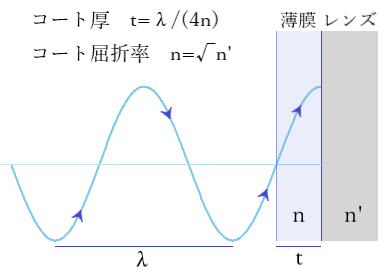
20.単層膜で反射防止コートを施すとき、理想的な反射防止膜の屈折率とコート厚の条件は?
【解説】
実際には、理想に近い屈折率の素材が使用され、機械強度や他の物性も考慮され、特定の波長以外にも有効となるように多層膜が施されますが、基本的な原理を示しますと以下のようになります。
- 先ずは「振幅条件」です。
反射率Rがゼロとなる時、n空気×nレンズ=n薄膜2 が成り立ちます。n空気=1.00として「nレンズ=n薄膜2」となります。
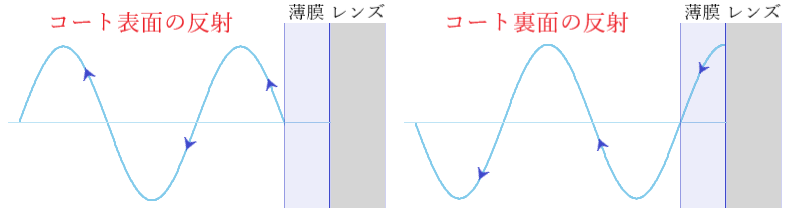
- 次に「位相条件」です。
コート表面と裏面の2つの反射が半波長のずれにより、光波が打ち消され反射がなくなります。
21.
【解説】
22.
【解説】
23.
【解説】







コメント メールアドレスが公開されることはありません。*が付いている欄は必須項目です。