Last Updated on 5年 ago by 管理者
フィボナッチ数列とは
自然界の現象に数多く出現する数列であり、その数列が生み出す螺旋は、最も美しい螺旋といわれております。
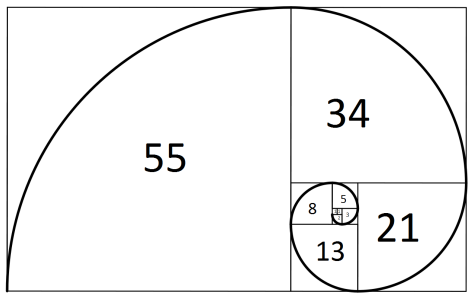
『フィボナッチ数列』とは、イタリアの数学者である、Leonardo Fibonacci、Leonardo Pisano(レオナルド・フィボナッチ、本名レオナルド・ダ・ピサ)さんが発行した『算盤の書』に記されていたものです。
実際の数列としては、
『0,1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181…』
です。
例えば、『第3項は、第1項と第2項の和』であり、『第4項は、第2項と第3項の和』、『第5項は第3項と第4項の和』…という規則性があります。
- F0 = 0
- F1 = 1
- Fn+2 = Fn + Fn+1
- n≧0の自然数
計算例としてn=5の場合はF7が求められ、F5+2=F5+F5+1=3+5=8となります。
以下の円グラフは、第1項から第100項まで求め、その割合を示したものです。
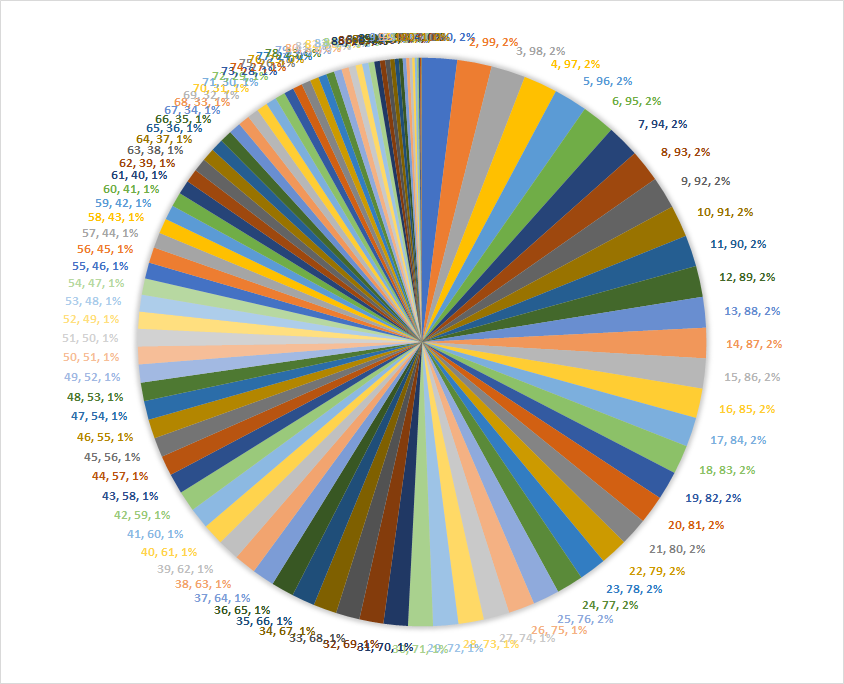
ここで、面白い事に、第1項から第80項の割合というのは、全体の2割となっている事です。
つまり、数字が大きい上位20項で全体の81.2%が占められています。
ここで、思い出される事としては、
売上高、コスト、在庫などの指標を大きい順にABCとランク付けし、管理する時に使う『ABC分析』です。
『ABC分析』は、『パレートの法則』に基づいたフレームワークです。
パレートの法則
『20:80の法則(80:20の法則)』や『ばらつきの法則』とも呼ばれます。
イタリアの技師、経済学者、社会学者、哲学者である、Vilfredo Frederico Damaso Pareto(ヴィルフレド・フレデリコ・ダマソ・パレート)さんが提唱しました。
経済学において「全体の数値の大部分は、全体の中の一部の要素が生み出している」という経験則です。
例えば、全商品の売上げの80%は、上位20%の商品や顧客で占められる…などです。
一方で『ロングテールの法則』というのもあり、インターネットマーケティングなどでは、ほとんど売れない下位20%の重要性というのも唱えられています。
フィボナッチ数列の例
- 兎の増え方
- 1ヶ月で1つのつがいの子を産む
- 1ヶ月で成長し、繁殖可能になる
- 親も死なず、毎月子を産む
- つがいの数が『フィボナッチ数』
- 枝の数
- 根本から上方にいくにつれ『枝分かれ』していき、その同じ高さでの本数合計が『フィボナッチ数』
- 花弁の枚数
- 3枚・・ユリ、アヤメ
- 5枚・・サクラソウ、キンポウゲ
- 8枚・・コスモス、デルフィニウム
- 13枚・・マリーゴールド
- 21枚・・チコリー
- 34枚・・オオバコ
- 55枚・・ユウゼンギク
- 89枚・・デイジー


- ひまわりの種・・螺旋状に21個、34個、55個、89個と並ぶ
- 松ぼっくりの鱗模様・・半時計回りに13回、時計回りに8回
- パイナップルの螺旋・・時計回りに13回、半時計回りに8回


- 為替のテクニカル分析の1つ
- フィボナッチ・リトレースメント
- 0.0%、23.6%、38.2%、50%、61.8%、100%
- 反応しやすいレート
- フィボナッチ数列の隣り合う数字の比率が1.618








コメント メールアドレスが公開されることはありません。*が付いている欄は必須項目です。