Last Updated on 4年 ago by 管理者
- 調節
- 【問1】調節力が8.00D、眼鏡度数S+3.00Dで完全補正される遠視眼の、裸眼での明視域と調節域は?
- 【問2】調節力が2.00D、S−5.00Dで完全補正される近視眼の、二重焦点レンズ度数S−5.00D Add+2.50の眼鏡装用でのおおよその明視域は?
- 【問3】自身の調節力2.00Dの半分を使用し、S−5.00Dで完全補正される近視眼の、二重焦点レンズ度数S−5.00D Add+2.50の眼鏡装用でのおおよその明視域は?
- 【問4】自身の調節力2.00Dの半分を使用し、S−5.00Dで完全補正される近視眼の、二重焦点レンズ度数S−5.00D Add+1.50の眼鏡装用でのおおよその明視域は?
- 【問5】遠点が眼後66.7cm、近点が眼前12.5cmの人の調節力は?
- 【問6】Donder’s(ドンダース氏)の表から予想される50歳の調節力はどの位?
- 視力
- 【問1】標準視標であるLandolt(ランドルト)環は最小〇〇閾?
- 【問2】ある正視眼の被検者が測定距離5mで、ランドルト氏環の直径15.0mmより小さい視力表を正読できない場合、小数視力は?
- 【問3】測定距離5mでランドルト氏環の直径7.5mmが正読可能である場合、3mでの距離に換算すると直径何ミリの視力と同等といえますか?
- 【問4】5m距離用の0.5視標を、3mで判別できた人の視力は?
- 【問5】LogMAR=1.0の視力は、小数視力でいくつ?
- 【問6】黄斑部中心窩に結像した場合に視力が良好となる理由は?
- 【問7】普通第一種免許の更新時、片眼視力0.3未満、若しくは片眼が見えない場合の条件は?
- こちらの記事も人気です。
調節
【問1】調節力が8.00D、眼鏡度数S+3.00Dで完全補正される遠視眼の、裸眼での明視域と調節域は?
- 明視域は、無限遠方~眼前20.0cm
- 調節域は、眼後33.3cm~眼前20.0cm
- 特に、装用距離が12mmである場合には・・・
- 明視域は、無限遠方~眼前20.5cm
- 調節域は、眼後32.13cm~眼前20.5cm
【解説】
眼鏡の装用距離を無視した場合には、単純に【 D=1/f 】、もしくは【 f=1/D 】で計算すれば良いです。
無限遠方を明視する為に、約+3.00の調節力を使用し、残りの5.00の調節力で近方を明視します。
遠点は1/+3.00≒0.333[m]
近点は1/(8.00−3.00)=0.2[m]
となります。
特に、設問では装用距離を何ミリでという条件はありませんでしたが、日本で一般的な12mmである場合には数字的に違いが出てきます。
装用距離が離れるほどに凸方向に補正度数が変化し、逆に近づくほどに凹方向に度数が変化するからです。
例えば、コンタクトレンズと眼鏡の度数が異なる原因の1つが、この装用距離による違いです。
近方視が困難になってきたシニアグラス(老視用の眼鏡)の装用距離を離すと、以前のように近方が見えやすくなる理由と同じです。
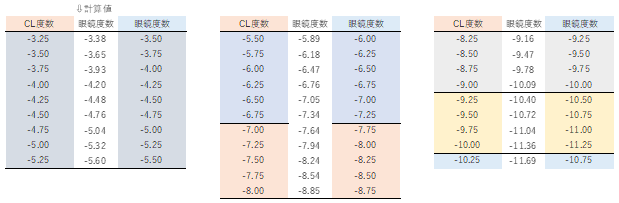
この度数の違いは、公式【 D/(1−d[m]×D) 】から計算できます。
眼鏡度数S+3.00D(装用距離12mm)で完全補正されるという事は、眼の屈折要素は−3.00より強いという事です。
実際に計算しますと、
(+3.00)/{1−0.012×(+3.00)}≒3.1120[D]
となり、約+3.11[D]の遠視眼である事がわかります。
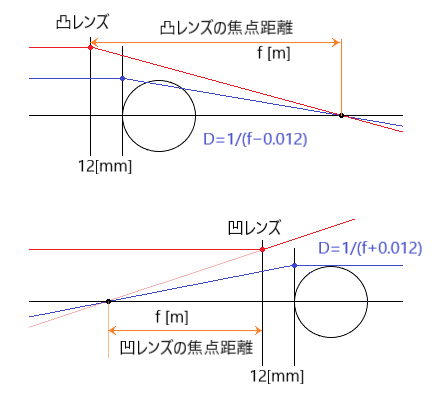
別解】 S+3.00[D]の焦点距離が1/3=約33.3[cm]である事から、以下の図のように考えて、
1/{1/3−0.012}=750/241≒3.1120[D]と計算しても良いです。
注】 焦点距離1/3を0.333として計算すると誤差が出ますので、分数のまま計算しましょう。
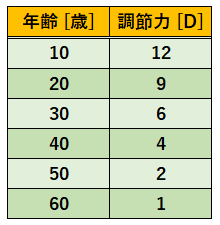
因みに、調節力8.00[D]はおよそ20代です。
そして、近点が眼前20cmとはいえ、最大調節力での明視ですので維持するのは辛く、長時間は疲れますね。
【問2】調節力が2.00D、S−5.00Dで完全補正される近視眼の、二重焦点レンズ度数S−5.00D Add+2.50の眼鏡装用でのおおよその明視域は?
- 無限遠方~眼前50cm、眼前40cm~眼前22.2cm
【解説】
二重焦点レンズの遠方部での遠点~近点は、
無限遠方~1/2.00[D]=0.50[m]です。
一方で近方部での遠点~近点は、
1/2.50[D]=0.40[m]~1/(2.50+2.00)=1/4.50≒0.222[m]です。
つまり、眼前50cm~眼前40cmは視界がジャンプします。
【問3】自身の調節力2.00Dの半分を使用し、S−5.00Dで完全補正される近視眼の、二重焦点レンズ度数S−5.00D Add+2.50の眼鏡装用でのおおよその明視域は?
- 無限遠方~眼前100cm、眼前40cm~眼前28.6cm
【解説】
二重焦点レンズの遠方部での遠点~近点は、
無限遠方~1/1.00[D]=1.00[m]です。
一方で近方部での遠点~近点は、
1/2.50[D]=0.40[m]~1/(2.50+1.00)=1/3.50≒0.286[m]です。
つまり、眼前100cm~眼前40cmは視界がジャンプします。
最大調節を長時間維持するのは疲れますので、およそ自身の調節力の半分を目安に処方すると良いでしょう。
二重焦点レンズの良い点は、累進多焦点レンズと比べて周辺部の歪みが無く視界が広く、明視するレンズ位置がわかりやすい事です。
【問4】自身の調節力2.00Dの半分を使用し、S−5.00Dで完全補正される近視眼の、二重焦点レンズ度数S−5.00D Add+1.50の眼鏡装用でのおおよその明視域は?
- 無限遠方~眼前100cm、眼前66.7cm~眼前40cm
【解説】
加入度数を必要以上に強く処方する事でのデメリットが多くあります。
明視する事が出来ない距離が存在してしまいます。視界がジャンプします。
仮に、自身の最大調節力を使用した際の明視域は、
遠方部では、無限遠方~眼前50cmとなり、
近方部では、眼前66.7cm~眼前28.5cmとなります。
適正な加入度数にする事で、視界のジャンプが無くなります。
累進多焦点レンズでも同様に、『近方が見えないから強く処方して欲しい』というお客様の話をそのまま素直に加入度数を強くしていくのはお勧めしません。
〇が書かれた鏡を使用した『ミラー法』や、顎を上げてもらう等の方法で近方視線を確認しましょう。

また、近用度数の処方を弱く下げるほど、明視可能な距離の幅が狭くシビアになります。
例えば、S−5.00Dで完全補正される近視眼(調節力2.00とする)に、近用眼鏡処方として2つの例を挙げます。
眼鏡処方をS−3.50Dとした際の明視域は、
眼前66.7cm~眼前28.6cmであり、その幅は38.1cmであるのに対し、
眼鏡処方をS−3.00Dとした際の明視域は、
眼前50.0cm~眼前25.0cmであり、その幅は25cmとなります。
このように、距離の幅自体が少なくなります。
また、像が拡大される事により視野が狭くもなりますので、より顔を動かす必要がでます。
【問5】遠点が眼後66.7cm、近点が眼前12.5cmの人の調節力は?
- 9.50D
【解説】
遠点から、f遠=1/0.667≒1.499[D]
近点から、f近=1/0.125≒8.00[D]
よって、遠点が眼前ではなく、眼後である事から遠視眼であり、無限遠方視の為に1.499[D]使用し、近見で更に8.00[D]使用できることから、これらを足し合わせ1.499+8.00≒9.50[D]となります。
調節力テストは、『マイナスレンズ付加法』と『ドンダーズのプッシュアップ法』などがあります。
マイナスレンズ付加法によるものは、マイナスレンズ付加による視標の縮小の為に調節力過小評価になり易くなります。
一方で、プッシュアップ法は、相対距離拡大により網膜像が拡大される事で調節力が大きめに測定される傾向になります。
そして、調節力テストの値が正常でも、全体的に調節が機能していない事もあります。
【問6】Donder’s(ドンダース氏)の表から予想される50歳の調節力はどの位?
- 2.50D
【解説】
年齢と調節力の関係を示した研究は様々あります。
石原氏、福田氏、Donder’s、Duane、Hofstetterなどが有名です。
以下に石原氏とドンダーズ氏のデータを並べて表に示します。調節力は減衰するものであり、このような差が出てしまうのは仕方がない事ですが、測定時の参考になります。
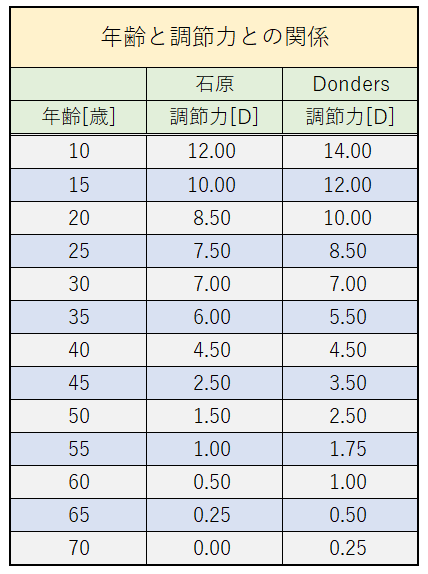
Hofstetterは、以下に示す『ホフステッターの公式』として、年齢による調節力との関係性でも広く知られております。
- (平均調節力)=18.5−0.3×(年齢)
- (最小調節力)=15−0.25×(年齢)
視力
【問1】標準視標であるLandolt(ランドルト)環は最小〇〇閾?
- 最小分離閾
【解説】
閾値(いきち)とは、境界となる値の事です。
視力は、眼の解像度の閾値で表します。『最小分離』で表す他には、『最小可読』『最小視認』『副尺視力』があります。
Landolt環の他に、Ferree-Rand環、Snellen鉤、井上鉤、Bostrom鉤、ローマ字視標、市松模様視標などもあります。

【問2】ある正視眼の被検者が測定距離5mで、ランドルト氏環の直径15.0mmより小さい視力表を正読できない場合、小数視力は?
- 0.5
【解説】
視力は、視角[分]の逆数で表されます。
例えば、視角1分[ ′ ]を視力1.0とします。
視角2′では視力0.5となり、視角5′では視力0.2となります。

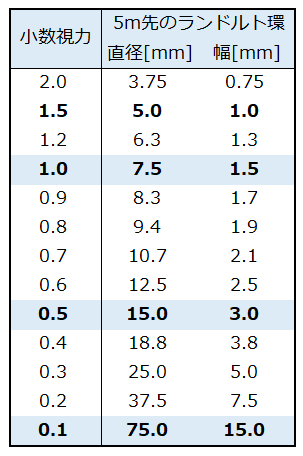
ランドルト氏環の直径が15.0mmという事は、上図より視角が2分となりますので視力は0.5となります。
以下の公式で視力を求める事ができます。
- 小数視力=7.5÷(直径)
- 小数視力=1.5÷(幅)
小数視力とLandolt環の大きさは以下の表に示します。
【問3】測定距離5mでランドルト氏環の直径7.5mmが正読可能である場合、3mでの距離に換算すると直径何ミリの視力と同等といえますか?
- おおよそ直径4.5mm
【解説】
5m視標で直径7.5mm、幅1.5mmの分離が判別できる際の視力は1.0です。
仮に3m視標を作製する際には、下図のように、5m視標の5分の3の大きさでランドルト環を作ると良いという事になります。
4m視標であれば、5分の4の大きさという事になります。
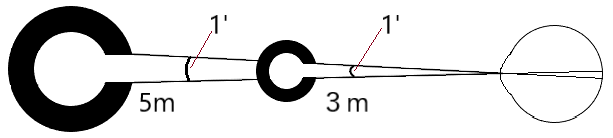
但し、近距離になると相対距離拡大により網膜像が拡大され見えやすくなります。
つまり、3m視標の方が良い視力と判断されやすくなります。
例えば、運転免許の更新用で3m視標で両眼視力0.7の眼鏡でも、5m視標で0.7の視力が無い場合もあり得ます。
【問4】5m距離用の0.5視標を、3mで判別できた人の視力は?
- 視力0.3
【解説】
0.5[視標]×3/5[m]=0.3[視力] となります。
以下に、視力に対するランドルト環の直径を、5mと3mで表にしたものを示します。
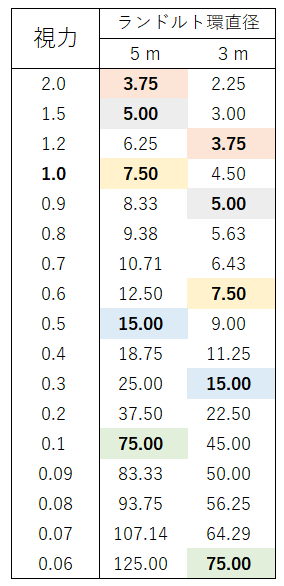
上図で、例えば視力0.5のランドルト環の直径は、5mでは15mm、3mでは9mmとなります。また、視力0.3では、5mは25mm、3mでは15mmとなります。
つまり、5m用の視力表を3mで見せた時の、0.5視標は視力0.3となります。
まとめますと、
5m用の2.0視標は、3mでは視力1.2
5m用の1.5視標は、3mでは視力0.9
5m用の1.0視標は、3mでは視力0.6
5m用の0.5視標は、3mでは視力0.3
5m用の0.1視標は、3mでは視力0.06
となります。
0.1以下の視力測定の場合、5m用の0.1視標を近づけて見える距離で測定することができます。
5m用の0.1視標は、5mでは視力0.1
5m用の0.1視標は、4mでは視力0.08
5m用の0.1視標は、3mでは視力0.06
5m用の0.1視標は、2mでは視力0.04
5m用の0.1視標は、1mでは視力0.02
5m用の0.1視標は、50cmでは視力0.01
となります。
また、それでも見えない場合には、30cmの距離で指の本数が判別可能か測定します。
それを指数弁といい、30cm指数、30cm/n.d.(n.d.=numerus digitorumの略)と表記します。
それでも判別不可の場合には、手動弁(眼前手動、m.m.=motus manus)、明暗(光覚)弁(s.l.=sensus luminis)、全盲(0)となります。
【問5】LogMAR=1.0の視力は、小数視力でいくつ?
- 0.1
【解説】
LogMAR視力とは対数視力の事です。
MAR ( Minimum Angle of Resolution )とは、最小可視角の事です。
対数視力と小数視力は以下の関係性があります。
Log MAR=Log (視角)=Log (1/視力)
Log MAR=1.0 の場合、
1.0=Log10(101) であり、101の部分が視角となります。
視角10分の視力は、小数視力=1/10=0.1となります。
◎対数の復習ですが、以下の関係が成り立ちます。
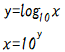
また、それぞれをグラフにしますと、以下のようになります。
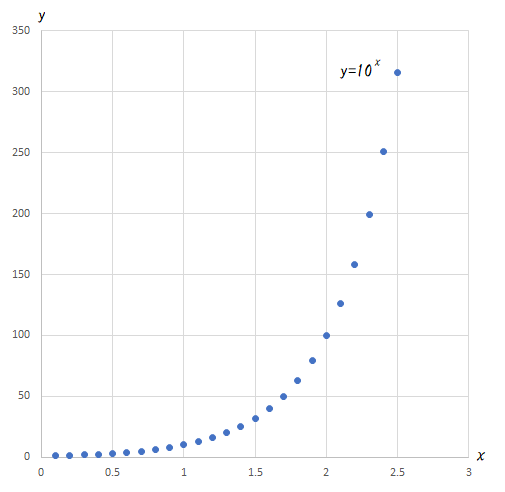
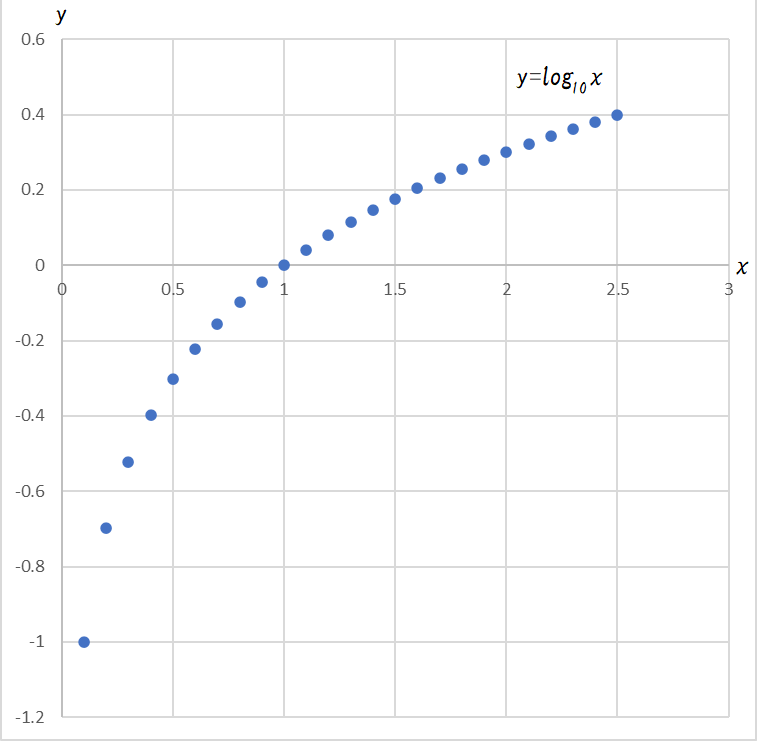
y=log10xとy=10xは、y=xに対して対称になります。
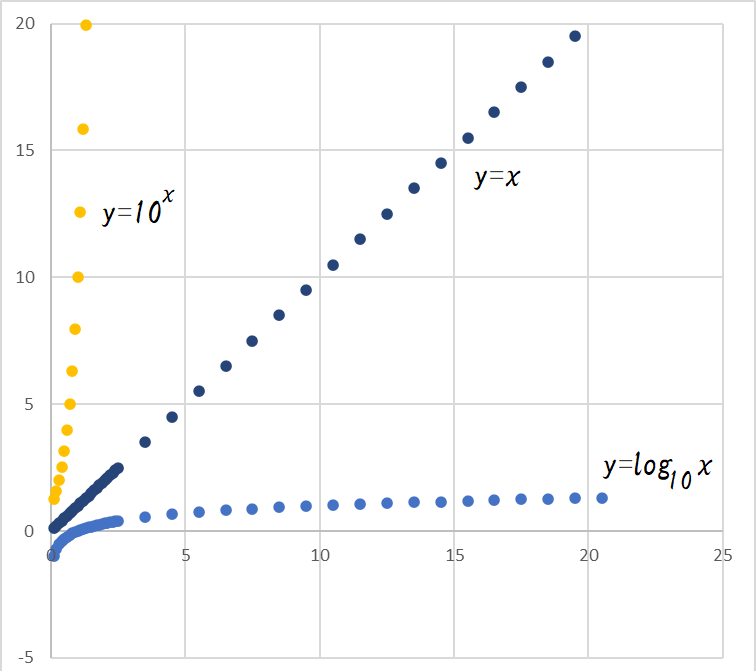
LogMAR視力1.0は小数視力0.1ですが、視力を対数で表記する良い点は、視力の間隔と大きさの間隔が等しくなる事です。
その為、視力の良し悪しに関わらず、等しく比べる事ができます。
小数視力の場合には、低視力の場合には通常視力と等しく比べる事ができません。
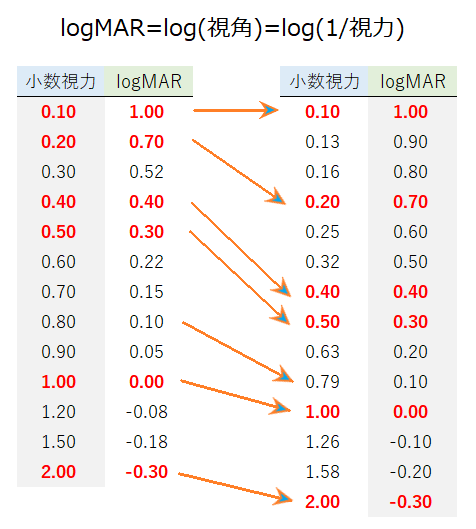
例えば、以下のように小数視力0.1と0.2の大きさの差は、小数視力0.9と1.0の大きさの差は等しくありません。
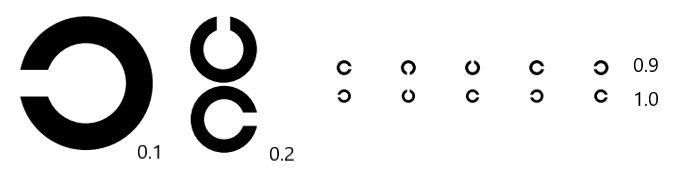
LogMAR視力表の場合には、大きさが約1/1.26倍(1010/2倍)と一定となります。
以下に、視力0.1間隔の小数視力とLogMAR視力を比較したものを示します。
【問6】黄斑部中心窩に結像した場合に視力が良好となる理由は?
- 黄斑部では脳層が薄く、錐体のみから成る為
【解説】
中心窩の錐体は、1つの双極細胞および1つの神経節細胞と1:1で連絡します。
周辺部の錐体では、1つの双極細胞に多数の錐体あるいは桿体が連絡し、更には、この双極細胞のいくつかが1つの神経節細胞と連絡します。
その為、中心窩からズレると視力は急激に低下します。
中心から2°ズレると、およそ視力1.0が0.5となり、
5°ズレると視力は0.3、10°ズレると視力0.2、20°ズレると視力0.1になるともいわれます。
例えば、網膜対応異常の場合には視力が出づらくなります。
【問7】普通第一種免許の更新時、片眼視力0.3未満、若しくは片眼が見えない場合の条件は?
- 視力が0.7以上であり、視野が左右150度以上である事
【解説】
普通第一種免許の更新では、ランドルト環視標で、片眼視力0.3以上、両眼視力0.7以上が必要となります。
片眼視力が出ない場合には、上記を満たす事で、更新自体は通ります。
しかし、個人的には、状況判断能力の低下などもあり得ますので免許更新が通りさえすれば良いという甘い考えは辞めて欲しいと考えます。
年齢と共に、一般的には視力の低下は起こります。しかし、80歳の1割程度の方は視力1.0あるともいわれております。





コメント メールアドレスが公開されることはありません。*が付いている欄は必須項目です。