Last Updated on 2年 by 管理者
クロスシリンダーテストは乱視の測定をする時に行います。
では、どういう理論で『乱視の軸度』と『乱視の度数』が決まるのかを学んでいきましょう。
今更もう遅いとか思わずに、知っている人も復習してみましょう。学習に遅いとかはないですからね。
クロスシリンダーテストの測定手順
クロスシリンダーを使った屈折測定の測定手順には、パスカル（Pascal. J. I）とコーポランド（Copeland. J. C）の測定方法があります。
パスカル （Pascal. J. I）の方法
乱視度数を増加することのみを考えた方法です。
乱視ゼロの状態を出発点として測定を開始するため、調節休止状態で最小錯乱円視をさせます。
コーポランド（Copeland. J. C）の方法
乱視度数を減少することのみを考えた方法です。
他覚測定値（または、今まで使用していた眼鏡度数）を出発点として測定を開始するため、マイナス乱視度数を減らすことを考慮し、遠視状態にすることで調節させ最小錯乱円視をさせます。
ほとんど調節力が無い60歳以上の人には適用できないものとなります。
クロスシリンダーレンズの構造
図(クロスシリンダー±0.50D)のような、度数の絶対値が等しいプラスとマイナスの円柱レンズを、互いにその軸が直行するように組み合わせたレンズです。
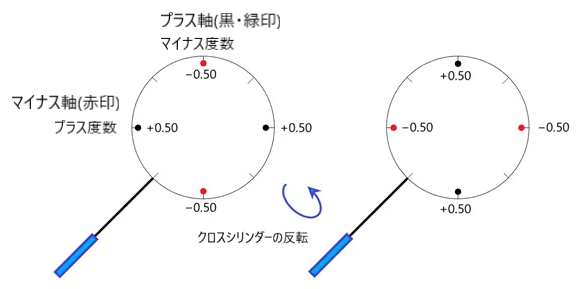
手持ちの軸を反転させると、プラスとマイナスの符号が変わります。
屈折測定には±0.25Ｄ、±0.50Ｄ、±0.75Ｄ、±1.00Ｄなどのレンズが使用されます。
クロスシリンダーレンズの各経線方向の屈折力の変化を図にしますと以下のようになります。
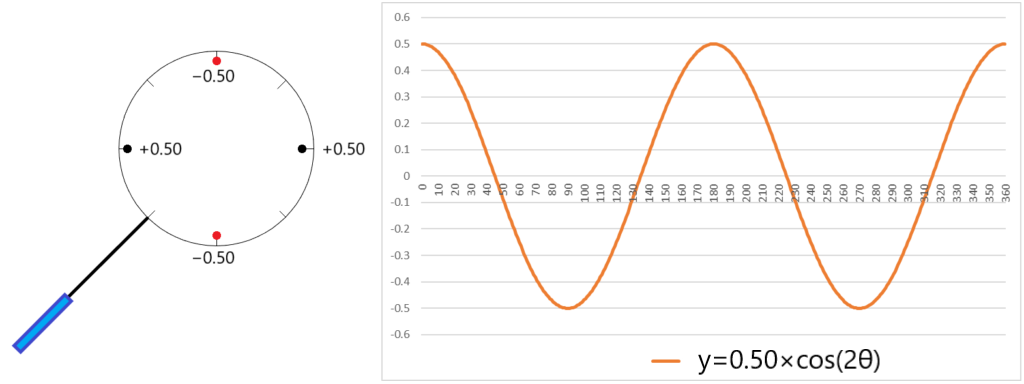
反転させると、以下のようになります。
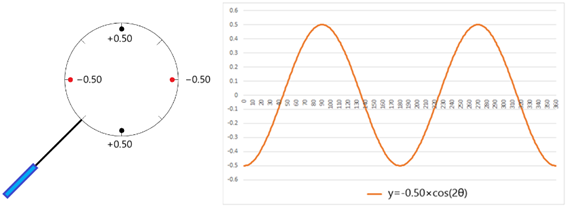
反転させることにより、どの方向でも度数が逆転しているのがわかります。
クロスシリンダーテストの理論
クロスシリンダーテストを行う際には、最小錯乱円視の状態にしないといけません。
クロスシリンダーは反転させても、最小錯乱円の『位置』は変わらないレンズです。
ただし、反転させることにより、最小錯乱円の『大きさ』は変わります。
最小錯乱円視をさせる為には、RGテストによる『R≦G』でも良いですし、単純に球面度数を付加していき、『プラス寄りの最高視力』の状態でもどちらでも良いです。
コーポランドの方法であれば、−0.50Dほど過補正の状態にします。
実際に、『C−1.00 Ax30°で補正される近視眼』で乱視補正を考えてみます。
C−1.00 AX30°で補正されるという事は、眼の要素としては『C+1.00 Ax30°』ということになります。
裸眼の状態では以下のようになります。
最小錯乱円視をさせる為に、『S−0.50Dを付加』すると以下のようになります。
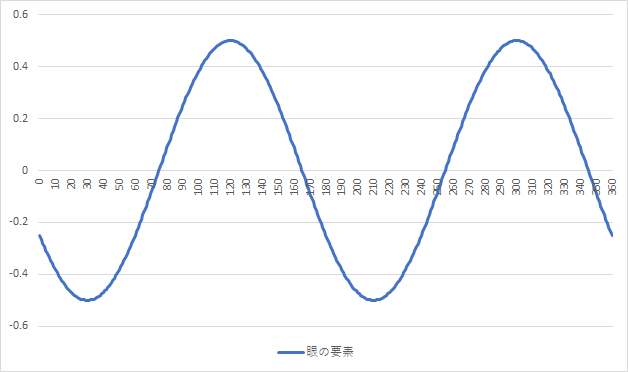
この最小錯乱円視の状態で『クロスシリンダー』を振っていきます。
乱視軸の決定
例えば、クロスシリンダーの『手持ち軸』を180°に合わせて①番と②番で反転させますと、それぞれ以下のようになります。
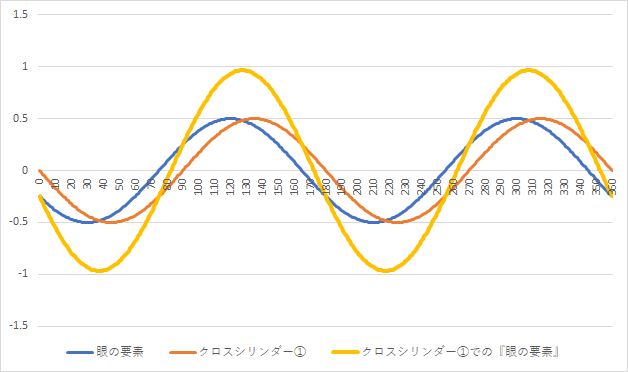
上図の『クロスシリンダー①番』では、『38°方向』に『1.93D程の乱視』が発生しています。
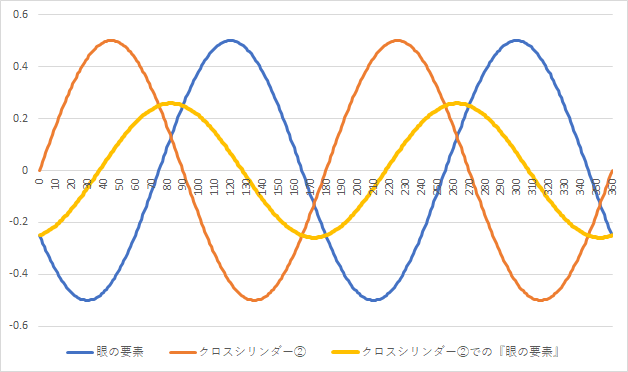
上図の『クロスシリンダー②番』では、『172°方向』に『0.52D程度の乱視』が発生しています。
②番の方が、ぼやけ具合（縦の大きさ：振幅）が少ないです。
そのぼやけ具合が少ない時の、クロスシリンダーレンズ『マイナス度数がある方向』に『本来の乱視軸』があります。
では、『手持ち軸』を30°に合わせてクロスシリンダーを反転させたときはどうなるのでしょうか。以下のようになります。
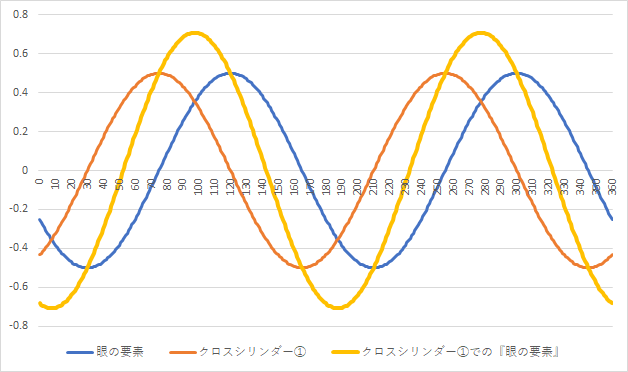
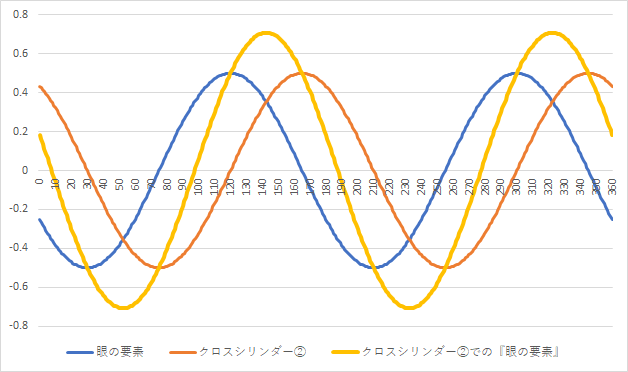
『手持ち軸』と『本来の乱視軸』が一致する場合には、①番と②番のぼやけ具合は等しくなります。
乱視度数の決定
乱視軸が決定しましたら、続いて乱視度数を決めます。
クロスシリンダーの度数が入る位置を『乱視軸』に合わせて、①番と②番で反転させます。
以下のようになります。
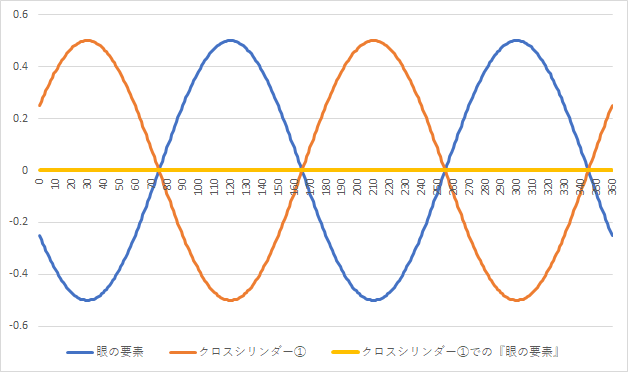
①番は、ぼやけが少なくなりました。この図では乱視なしになりました。
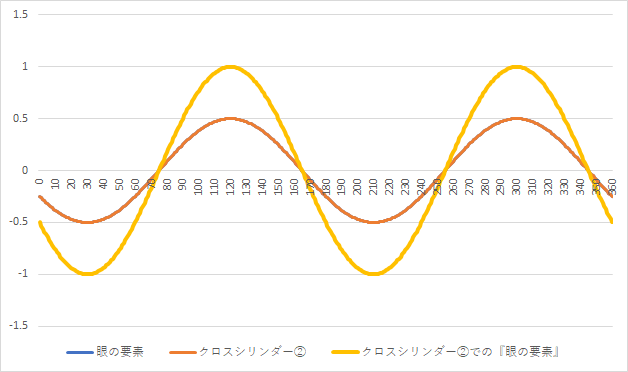
②番は、乱視が2.00Dに増えてしまい、ぼやけが増えてしまいます。
ぼやけが少なくなる①番は、『本来の乱視』が足りないということになります。
補足
クロスシリンダーの図ではありませんが、以下の様な図で理解してみても良いでしょう。
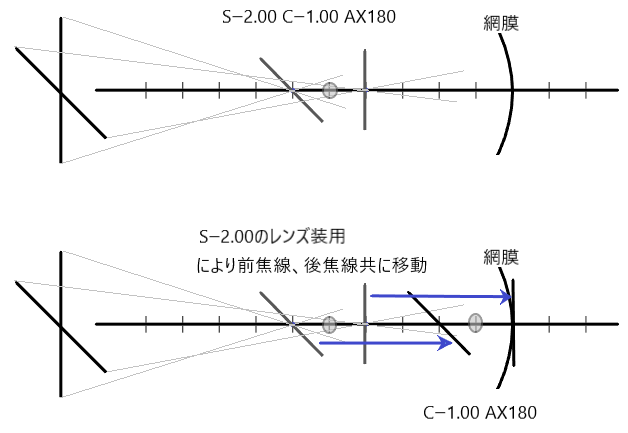
クロスシリンダーを反転させると、前焦線と後焦線がどう動くのか。
最小錯乱円の大きさがどうなるのか・・・考えてみてはいかがでしょうか。
コメント