Last Updated on 11か月 by 管理者
だいぶ前に投稿した『計算式のまとめ(よく使うもののみ)』をざっくりとリライティングしました。
眼鏡ブログを始めたばかりに投稿した内容で、こんなものを投稿していたなんて・・と恥ずかしくなりました。
こんな内容のものでもPV数が毎月1Kあり(自分の中では多い‼)、これはまずい!!と急いで画像などをUPしました。以前はこれが精一杯だったのでしょう。2023年12月現在でも毎月安定のPV数1Kがありますので、改めてリライトしますね。
拙さに気付けたということは、自分も成長しているのだと痛感します。これからもよろしくお願いいたします。
2021年の6月当時、一つのサイトで全て完結できる『1級眼鏡作製技能士の資格取得をサポート』するコンテンツを作成しておりますので(かなりのボリューム)お楽しみに!!・・・ということでしたが、⇨2023年に作製後、有料コンテンツにしようかと思いましたが辞めました。(笑)
度数Dと焦点距離f
既成の老眼鏡で+1.00Dや+2.00Dなどとよく目にする度数と焦点距離との関係は?
- 度数[D]=1÷焦点距離[m]
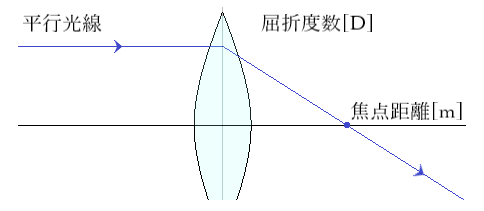
例題)屈折度数+3.00Dのレンズの焦点距離は?
1÷3.00[D]≒0.333[m]、つまり33.3cmとなります。
⦿ 正視眼(例えば、遠方視力良好)の方が、+3.00[D]の老眼鏡を掛けると、およそ近方距離33cmが楽に見えるようになります。
等価球面度数SE(Spherical of Equivalent)
⦿ 等価球面度数とは、最小錯乱円の位置が変わらないように、乱視度数の半分を球面度数に換算した度数です。
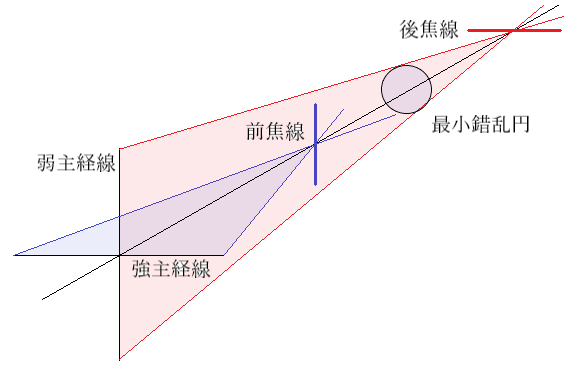
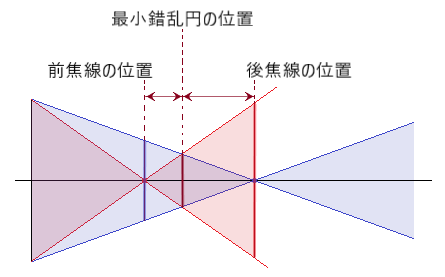
- 等価球面度数[D]=球面度数[D]+乱視度数[D]/2
例題)S−1.00 C+1.50 の等価球面度数は?
計算式】SE=−1.00+1.50/2=−0.25[D]
度数転換
眼科処方箋で、SとCの符号が異符号であることを良く見かけます。
混乱を避けるために、一般的に眼鏡店では、『SとCの符号を揃える』ことの出来る度数はそちらを優先して表示します。出来ない場合には『マイナスC表示』に統一します。
- S(A) C(B) Ax(C) ⇨ S(A+B) C(−B) Ax(C+90)・・・A,B,Cには数が入ります。
例題)S−1.00 C+1.50 Ax95 を度数転換すると?
計算式】S+0.50 C−1.50 Ax5『マイナスC表示』
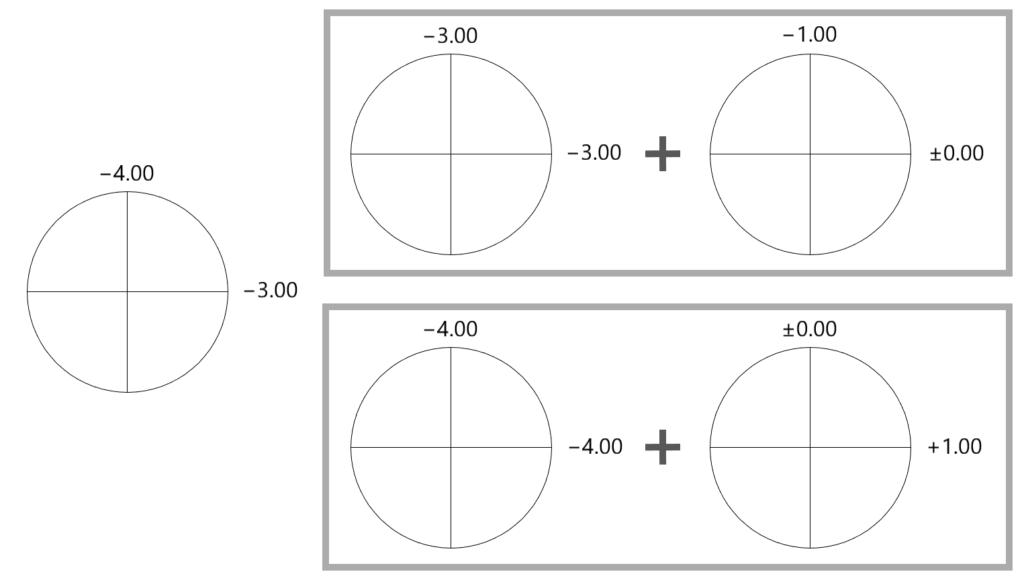
例題)S−3.00 C−1.00 Ax180 を度数転換すると?
『S−3.00』と『C−1.00 Ax180°』の2枚のレンズに分解できます。
また、『S−4.00』と『C+1.00 Ax90°』の2枚のレンズにも分解できます。
つまり、S−3.00 C−1.00 Ax180 を度数転換すると『S−4.00 C+1.00 Ax90°』になります。
遠点と近点の計算
- 遠点・・無調節状態の焦点距離[m]
- 近点・・最大調節状態の焦点距離[m]
- 焦点距離[m]=1÷度数[D]
- 度数[D]=1÷焦点距離[m]
例題)S−4.00[D]の近視、調節力6.00[D]の遠点と近点は?
遠点は、1/4.00=0.25[m]
近点は、1/(4.00+6.00)=0.1[m]
遠近両用メガネの加入度数 Addition
- 加入度数[D]=近用度数[D]−遠用度数[D]
例題)遠用度数 S−6.50[D]、加入度数1.50[Add] の近用度数は?
計算式】−6.50[D]+1.50[D]=−4.00[D]
- 加入度数Add=−1 / (作業距離)−(定数0~1)×調節力
- 定数・・焦点を合わせる為の自身の調節力をどのくらい使用するのかという割合。100%使用して明視するのであれば定数は1。もし半分の調節力を使用して近方視をする場合には0.5となります。
常に100%の調節をして明視している状態は疲労しやすいので、一般的には50%の調節力を使用するくらいに眼鏡度数を調整します。
調節Ac (Accommodation)
- 調節量[D]=(1/近点[m])−(1/遠点[m])
例題)S−3.00[D]の近視で、20cmの距離を見た時の調節量は?
計算式】20cmを見るときの度数は1/0.2[m]=5.00[D]ですので、調節量=5.00−3.00=2.00[D]
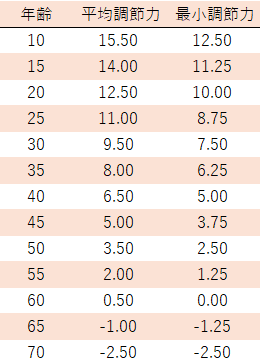
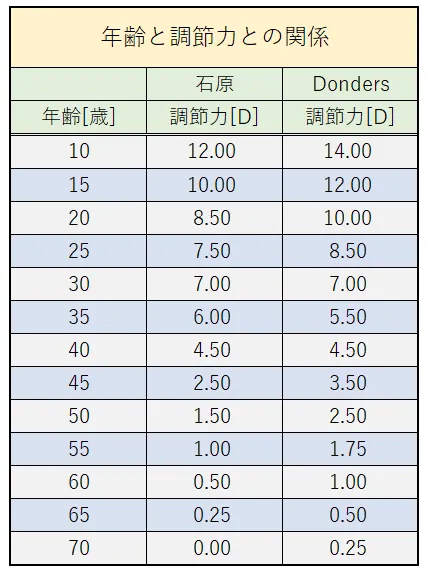
Hofstetterホフステッターの公式(年齢と調節力との関係性)
- (平均調節力)=18.5−0.3×(年齢)
- (最小調節力)=15−0.25×(年齢)
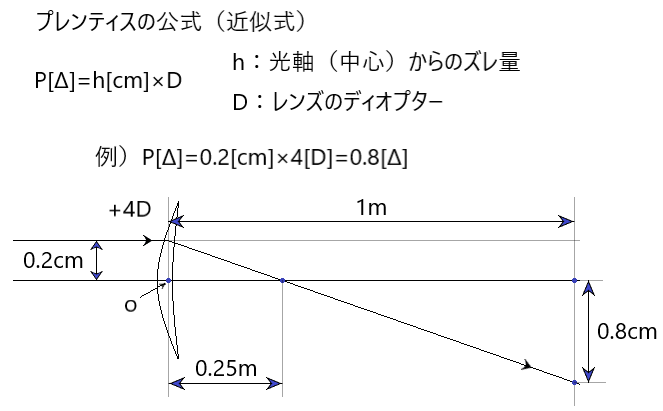
プリズム量(プレンティスの公式)
- プリズム作用[△]=光学中心からのずれた距離[cm]×度数[D]
- 1△では、1m先が1cmずれて見えます
例題)S+4.00Dのレンズで、光学中心から2mm離れた箇所のプリズム量は?
計算式】0.2[cm]×(+4.00)[D]=0.80[△]
例題)5△レンズは10m先がどの位ずれて見えるのか?
計算式】5[△]×10[m]=50[cm] なので、50cmずれて見えます。
プリズムの角度表示
sinθやcosθの計算は関数電卓が必要です。
その際にはDEGで計算しましょう。RADやGRADではないので注意してね。
先ずは、サインとコサインの復習から↓
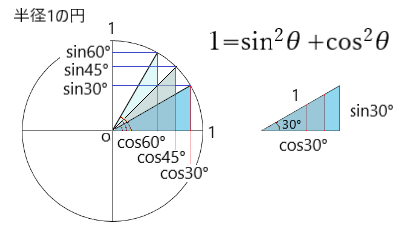
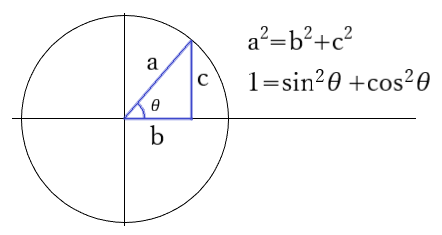
サインカーブを図にした場合には↓
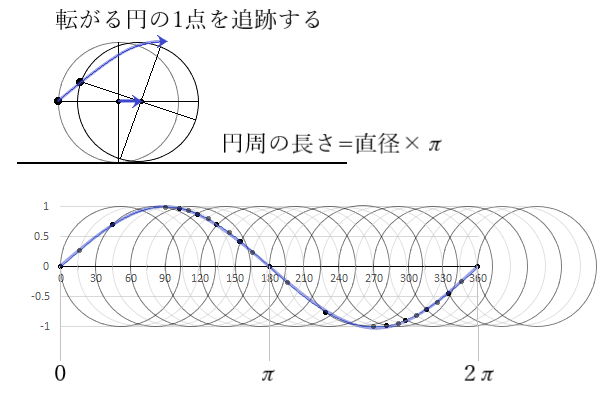
- プリズム度数P[△] 基底方向(角度)で表示される
- 水平方向(Px)は・・プリズム度数×cos(基底方向の角度)°
- 垂直方向(Py)は・・プリズム度数×sin(基底方向の角度)°
- P2=Px2+Py2
例題)右眼、2.25Δ B27°を『水平成分』と『垂直成分』に分解すると?
『水平成分』・・2.25Δ×cos27°≒2.00ΔBI、
『垂直成分』・・2.25Δ×sin27° ≒ 1.02ΔBU
から、
『水平成分』・・2.25Δ B27° ≒ 2.00Δ BI
『垂直成分』・・1.00Δ BU となります。
スコア表記での乱視度数
レンズのコバ厚を求める場合、球面度数と乱視度数を考慮して求めなければなりません。
乱視度数は以下のようなサインカーブを描きます。
- 円柱レンズの断面度数は sin2θ
- 断面度数は、球面度数+sin2θ
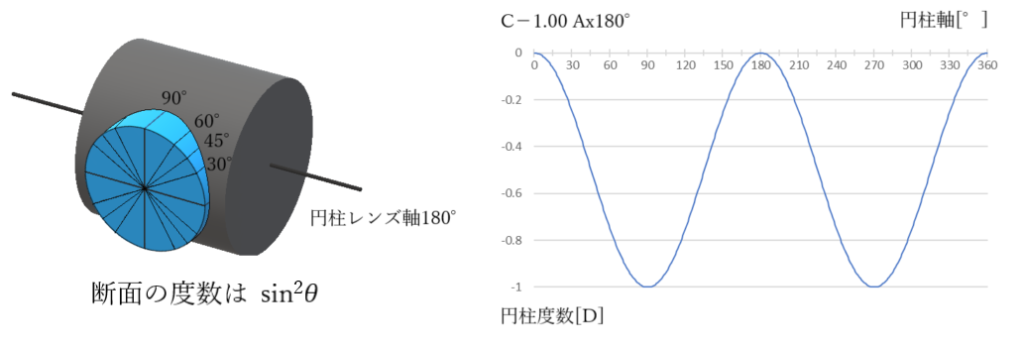
◎ 例えば、C−1.00 Ax180°をスコア表記しますと、以下のようになります。
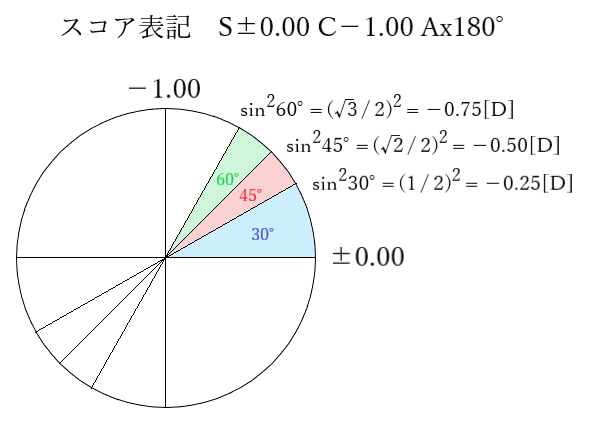
よって、各方向での度数は以下のように計算できます。
90°方向は−1.00[D]
60°方向は−1.00×3/4=−0.75[D]
45°方向は−1.00×1/2=−0.50[D]
30°方向は−1.00×1/4=−0.25[D]
180°方向は±0.00[D]
例題)レンズ度数 S−3.00 C−1.00 Ax30° の180°方向の度数は?
計算式・・−3.00+(−1.00×1/4)=−3.25[D]
例題) レンズ度数 S−3.00 C−1.00 Ax60° の180°方向の度数は?
計算式・・−3.00+(−1.00×3/4)=−3.75[D]
↓参考に、屈折率1.60、球面レンズ(60φ)の大まかな厚み表
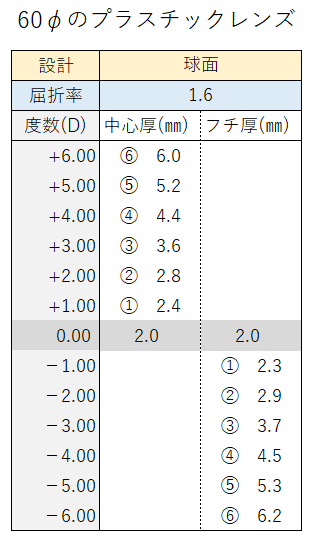
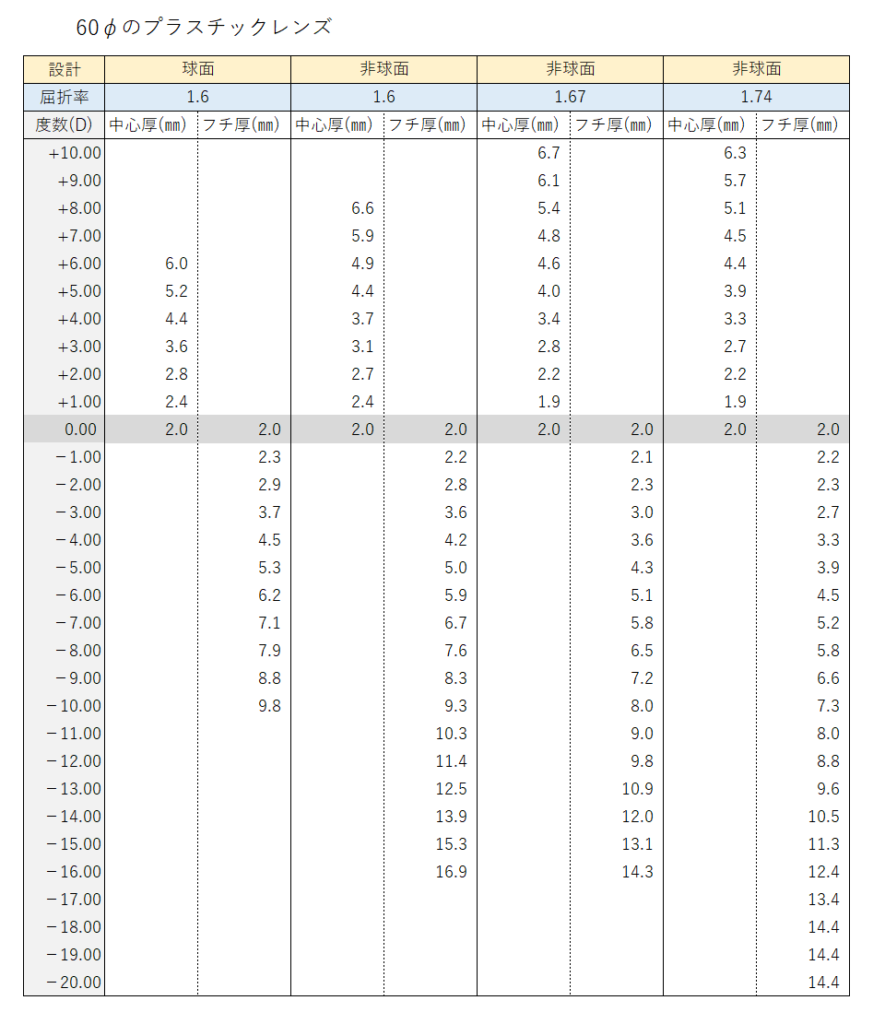
FPD
- FPD=玉形サイズ+ブリッジ幅
例題)ボクシングシステムで 53▢18-14 と表示されるFPDは?
計算式】FPD=53+18=71[mm]
※ ボクシング・システムとは、ISO(国際標準化機構)が採用した規格(ISO/FDIS5624)に基づき、日本でも採用された寸法測定法(1990年2月1日 JIS B 7282)です。
必要レンズ径
フレームが大きい場合や、右眼と左眼の距離が狭い場合には、レンズの光学中心と黒目の中心を合わせて加工しようとする時に、レンズの大きさが足りず削れない場合があります。
- 必要レンズ径=|FPD−PD|+玉形最長径+マルチリング幅(+加工上の余裕分)
例題)フレーム53▢18-14、加工PDが60mm、マルチリング3mmの時に必要となるレンズ径は?
(53+18)−60+53+3=67[mm] となりますので、凸レンズなどによくある65径の大きさのレンズをそのままでは加工できません。
『FPD−PD』の値がもし仮にマイナスの場合、そのまま計算してしまうと耳側の必要レンズ径を計算することになります。
FPD<PDの場合(マイナスの値)には、耳側よりも鼻側の方がレンズの大きさが必要になりますので注意!!
必要な偏心量
必要レンズ径が足りずに加工出来ない時には、レンズ光学中心を特注としてレンズメーカーに偏心してもらいます。
但し、偏心して加工自体は出来ますが、レンズの光学性能が落ちます。フレームサイズが自分には大きいと諦め、小さい枠に変更するのが本来は良いです。眼鏡販売店側も、面倒がらずに小さい枠をお勧めするのも、販売スキルのひとつです。
- 必要偏心量=(必要レンズ径−レンズ基準径)÷2(+余裕分)
例えば、必要レンズ径67mm、レンズ基準径65mmの必要偏心量は?
(67−65)÷2=1[mm] となります。レンズメーカーさんにお願いしても偏心がしっかりなされない場合も多く(弱度数やMIXは作成工程の関係で難しい・・)ですので、余裕をもって3mm~5mmくらいで偏心指定をしましょう。
角膜頂点間距離による度数換算
- D=D眼鏡/(1−D眼鏡×装用距離[m])
例題)S−8.00Dの眼鏡レンズを12mmで装用したときに完全補正される眼に対して、14mmまで離した時の必要となる補正効果は?
計算式】D=−8.00÷{1−(−8.00×(0.012−0.014))}≒−8.130081[D]
よって、約0.13[D]の補正不足になります。
例題)S−8.00Dの眼鏡レンズを12mmで装用したときに完全補正される眼に対して、0mmまで近づけた時の補正効果は?
計算式】D=−8.00÷{1−(−8.00×0.012)}≒−7.299270[D]
よって、約0.70[D]の過補正となります。これは、つまりコンタクトレンズ度数での換算値(装用距離≒0)ともいえます。
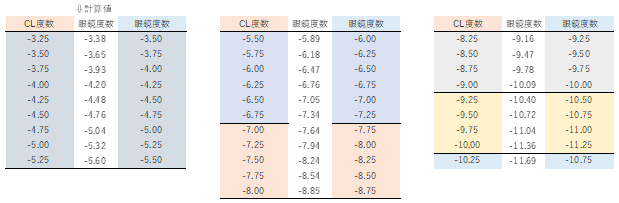
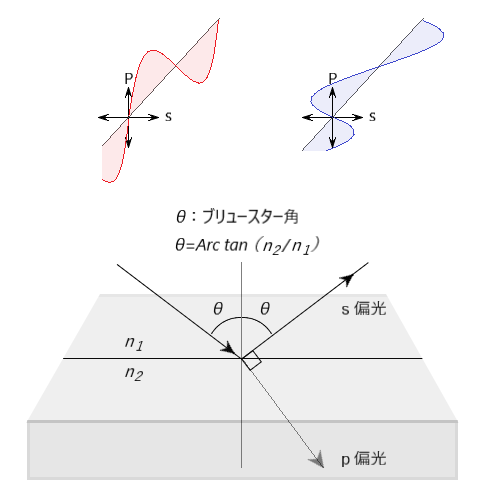
スネル(Snell)の法則
光が、媒質1(屈折率n1)から媒質2(屈折率n2 )へ入射(角度θ1)し、屈折(角度θ2)する時の法則
- n1×sinθ1=n2×sinθ2
例題)水中(屈折率1.33)から大気中(屈折率1)へ入射する時の、全反射が起きる最も小さい入射角(臨界角)は?
計算式】sinθ1/sinθ2=n2/n1に、臨界角はθ2=90°ですので、sinθ2 =1
sinθ1=n2/n1から、θ1=sin-1(1.00/1.33) ≒48.6°
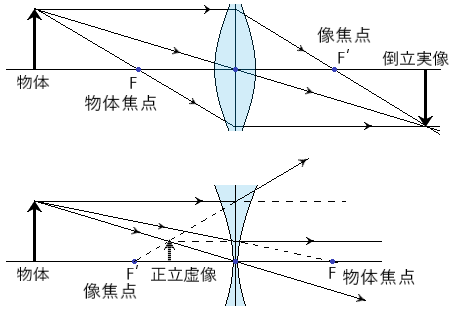
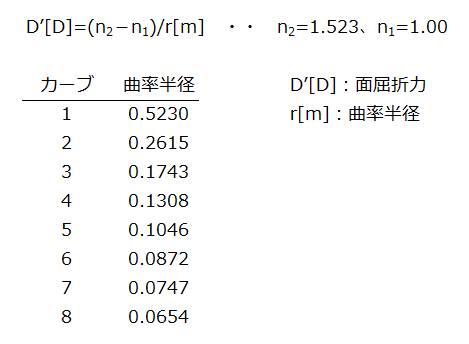
球面における屈折の式
- (n2/s2)−(n1/s1)=−n1/f1=n2/f2=(n2−n1)/r
- n・・屈折率
- s1・・物距離
- s2・・像距離
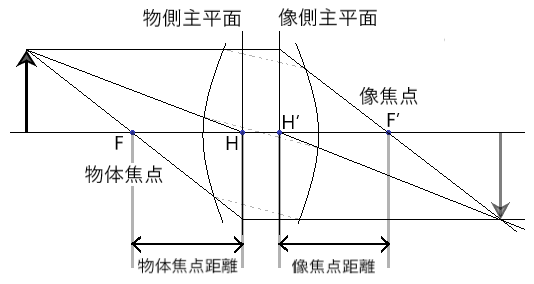
- f1・・物体焦点距離
- f2・・像焦点距離
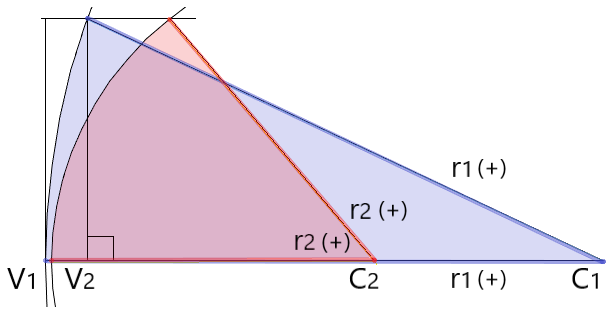
- r・・曲率半径
- D=D1+D2−(t/n)D1×D2
- D1・・レンズ前面の屈折力[D]
- D2・・レンズ後面の屈折力[D]
- n・・屈折率
- t・・レンズの厚み[m]
像の横倍率
- 横倍率=(s2−r)÷(s1−r)=(n1×s2)÷(n2×s1)
- β=y’/y=(s’-r)/(s-r)=ns’/n’s
- β:横倍率
- y:物体の大きさ
- y’:像の大きさ
実際の眼鏡倍率は、眼とレンズの距離が離れていますので、以下のような要因(眼鏡レンズの倍率)を考慮しないといけません。
眼鏡レンズの倍率
- SM=Mp×Ms={1/(1−lv×Dv)}×{1/(1−t/n×D1)}
- Mp・・Power factorの略で、パワーによる要因
- Ms・・Shape factorの略で、形による要因
- lv・・レンズ後面頂点から眼の入射瞳までの距離
- Dv・・レンズ後面頂点屈折力
- D1・・レンズ前面の屈折力
- t・・レンズの厚み
- n・・レンズの屈折率

例題)S+5.00 C−5.00 AX180 でレンズ後面がトーリック面、t=0.005[m]、n=1.5、D1=+8.00[D]、装用距離12mm(lv=0.015mm)とした場合の倍率は?
- MP=1÷(1−0.015×5.00)≒1.081081081
- MS=1÷(1−0.005÷1.5×8.00)≒1.027397264
以上から、180°方向はMp×Msから約1.111になります。
90°方向は同様に屈折力0.00[D]として計算すると約1.027になります。
よって、両主径の倍率差は8.4%になります。
ジャバルの式
ジャバルの式とは、角膜乱視の度数から全乱視の度数を推測する公式です。
- 全乱視=1.25×角膜乱視+(−0.50D AX90°)
例題)オフサルモメーターで角膜の曲率半径を測定した時の、以下の値から角膜乱視(補正するシリンダーレンズ)を求めよ?
角膜の主経線の屈折力は、42.50D@90° 43.75D@180°
解)
- C−1.25D Ax90°
- 強主経線は180°方向の43.75D
- 弱主経線は90°方向の42.50D
- よって、差は1.25でありマイナスシリンダー90°で補正します。
例題)角膜乱視がC−1.00D Ax180°の場合、ジャバルの式から予測される全乱視は?
解)
全乱視=1.25×角膜乱視+(−0.50D AX90°)
=1.25×(−1.00 Ax180)−0.50 Ax90
=−1.25 Ax180 − 0.50 Ax90
=−1.25 Ax180+0.50 Ax180=−0.75D AX180°
=+1.25 Ax90 − 0.50 AX90=+0.75D AX90°
例題)角膜乱視がC−1.00D Ax90°の場合、ジャバルの式から予測される全乱視は?
解)
全乱視=1.25×角膜乱視+(−0.50D AX90°)
=1.25×(−1.00 Ax90)−0.50 Ax90
=−1.25 Ax90 − 0.50 Ax90
=−1.75D AX90°
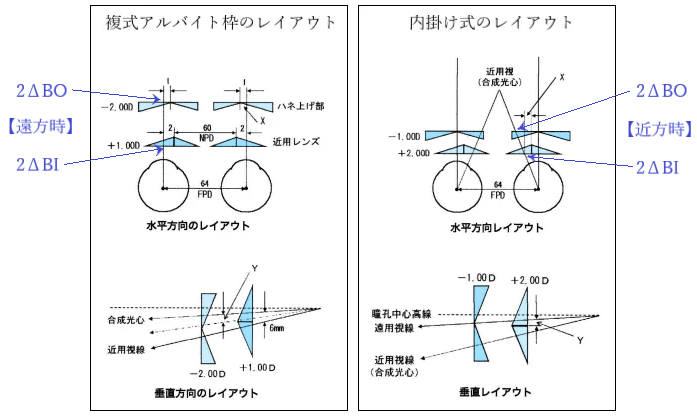
遠用ビジュアルポイント
遠用ビジュアルポイント(DVP:distance visual point)とレンズ光学中心の上下方向の偏位距離は以下の近似式で求めることができます。
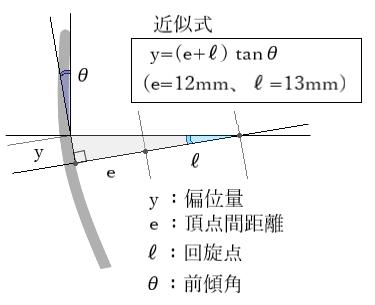
◎ 水平視線(第一眼位)から、遠用視線5°、常用視線10°、近用視線15°下方回旋します。
例1)前傾角 θ=5° の場合・・偏位量 yは (12+13)×tan5°≒2.2[mm]となる。
例2)前傾角 θ=10° の場合・・偏位量 yは (12+13)×tan10°≒4.4[mm]となる。
例3)前傾角 θ=15° の場合・・偏位量 yは (12+13)×tan15°≒6.7[mm]となる。
近用PD
近見時に、レンズ光学中心を通る為のPDは以下の図から、
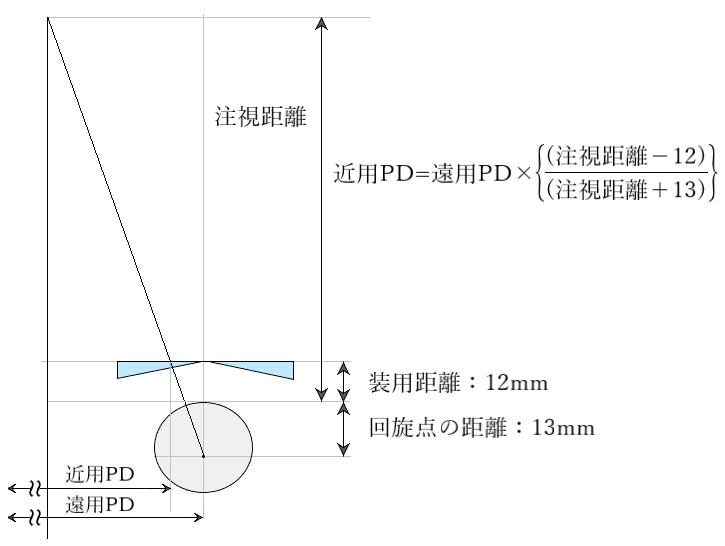
公式としては、次のようになります。

◎ 近用PDは、およそ遠用PDから 3±1[mm] 引いた値となります。
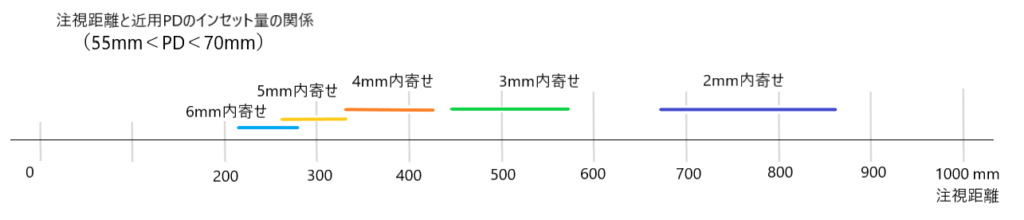
その他の公式
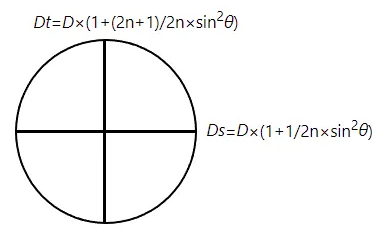











コメント メールアドレスが公開されることはありません。*が付いている欄は必須項目です。