斜交円柱の原理

Last Updated on 2年 by 管理者

補正する円柱レンズの軸方向をずらした場合には合成乱視が生じます。

放射線視標の見え方を例に、乱視軸の修正手順を以下に示します。

例えば、『S−0.50 C−1.00 Ax10°』で完全補正される眼について

先ずは、未補正のままで放射線視標を見た時は以下のように見えます。

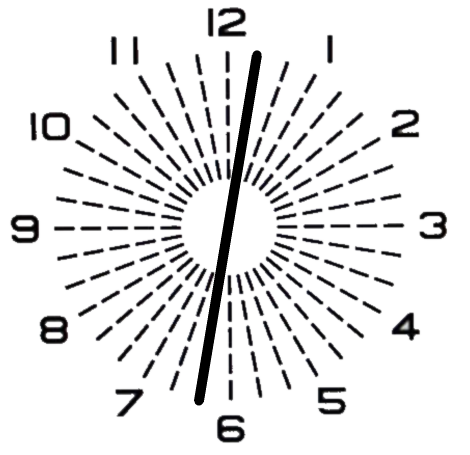
乱視軸の測定に誤りが無い場合

①　『C−1.00 Ax10°』を装用させた場合には、濃く見える方向の線は無くなります。

『C−1.25 Ax10°』を装用させた場合には、濃く見える方向の線は±90°方向逆転します。よって補正する乱視軸方向に誤りが無い、もしくは誤差の範囲内といえます。

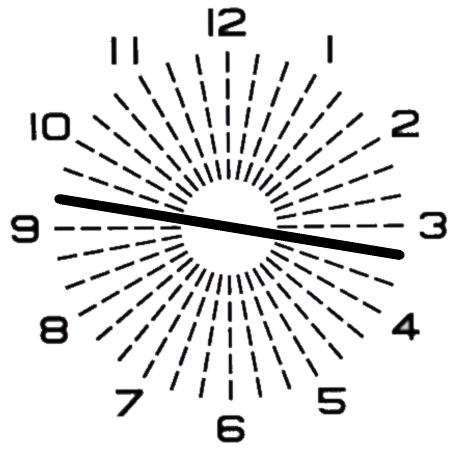
②　次に、『C−1.00 Ax10°』の乱視軸方向を、それぞれ『±10°』回転させた場合を考えてみます。

『C−1.00 Ax20°』を装用させますと『C−0.35 Ax150°』の残余乱視が発生します。

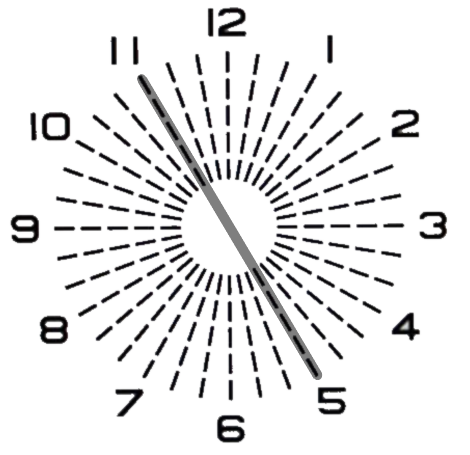
『C−1.00 Ax180°』を装用させた場合には『C−0.35 Ax50°』の残余乱視乱が発生します。

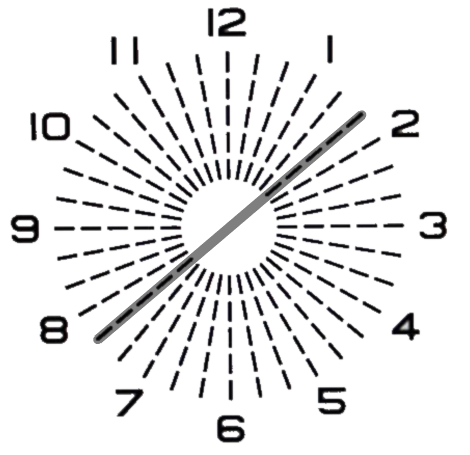
±10°方向ずらしても、濃く見える線が等しく40°方向ずれ、更には濃さも±10°で違いが無い事から、乱視軸の測定が上手く出来たといえます。

③　では、それぞれ『±30°』回転させた場合ではどうなるのかを考えてみます。

『C−1.00 Ax40°』を装用させますと『C−1.00 Ax160°』の残余乱視が発生します。

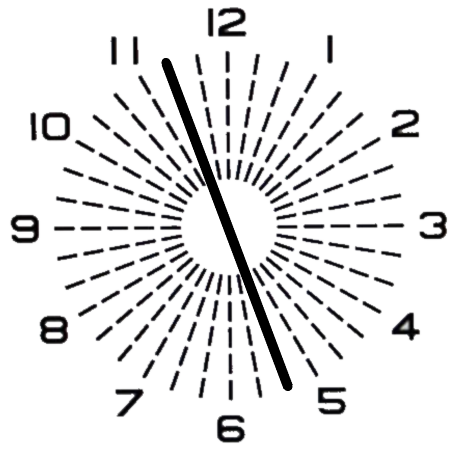
『C−1.00 Ax160°』を装用させた場合には『C−1.00 Ax40°』の残余乱視が発生します。

±10°方向ずらした場合と同じく、ズレ量と濃さが等しくなります。

乱視の測定に『S−0.50 C−1.00 Ax180°』という誤りがある場合の軸修正法

先ずは、本来の未補正度数『S−0.50 C−1.00 Ax10°』、裸眼にて放射線視標を見た時は以下のように見えます

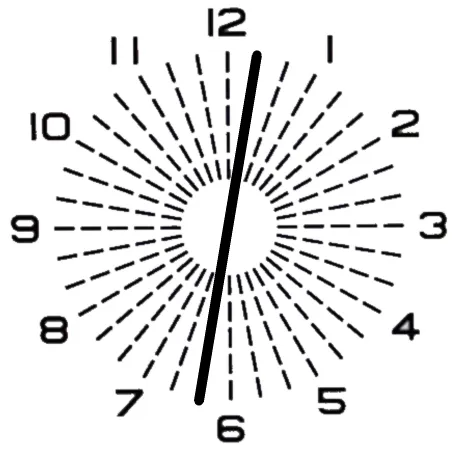
①.　測定の誤差などの原因により、『C−1.00 Ax180°』を装用させた場合には、『C−0.35 Ax50°』の残余乱視乱が発生します。

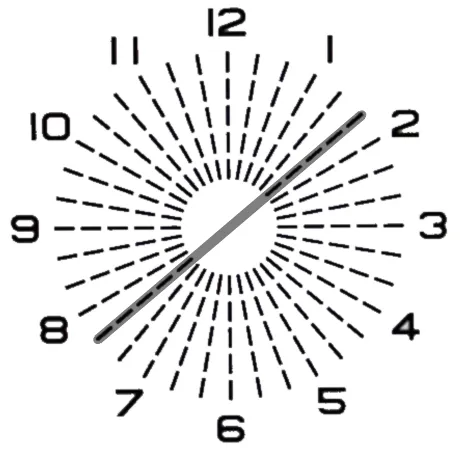
『C−1.25 Ax180°』を装用させた場合には、『C−0.46 Ax66°』の残余乱視が発生します。

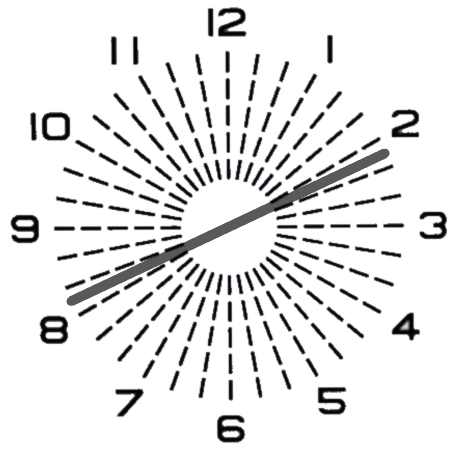
濃く見える方向が±90°方向逆転せず、別の方向がより濃く見えるという事から、測定に誤りがあると予想する事ができます。

一旦、『C−1.00 Ax180°』を装用させた状態に戻します。

②.　では、具体的に測定された乱視軸の修正をしていきます。
それぞれ『±5°』回転させた見え方を確認します。

円柱軸を+5°回転させた『C−1.00 Ax5°』を装用させますと『C−0.17 Ax53°』の残余乱視が発生します。濃さは弱くなります。

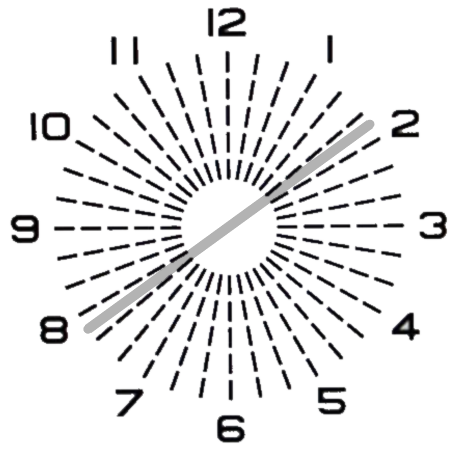
円柱軸を−5°回転させた『C−1.00 Ax175°』を装用させますと『C−0.52 Ax48°』の残余乱視が発生します。濃さは強くなります。

③　+5°回転させた『C−1.00 Ax5°』の方が濃さが均一に近づく為、そちらに軸修正をします。

④　更に、『±5°』回転させた見え方を確認します。

『C−1.00 Ax10°』を装用させますと濃く見える線が無くなります。乱視軸の修正が完了しました。

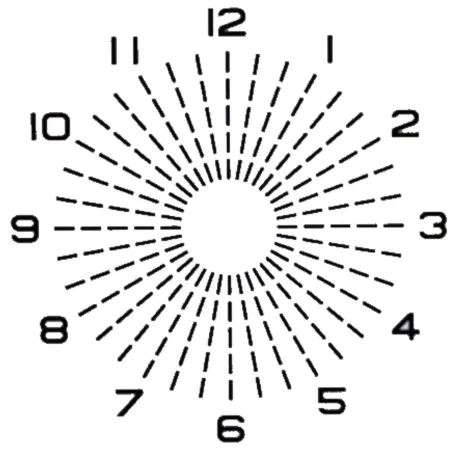
『C−1.00 Ax180°』を装用させますと『C−0.35 Ax50°』の残余乱視が発生します。

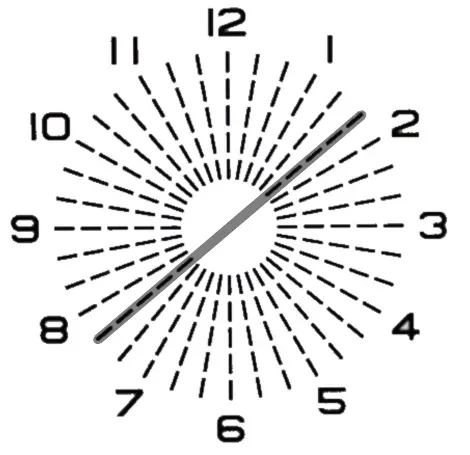
残余乱視が『C−0.17 Ax53°』から『C−0.35 Ax50°』になる為、濃さが強くなります。

円柱軸の修正方法

上の例では、『S−0.50 C−1.00 Ax10°』で完全補正される眼について円柱レンズの軸方向を±5°方向ずらし、濃さが薄くなる方向に修正しました。

理解を深める為に、別角度から考察してみます。

◎　本来『S−0.50 C−1.00 Ax10°』で完全補正される眼で、『C−1.00 Ax180°』が装用されている条件で再度考察していきます。

◎　今度は装用されている『C−1.00 』のレンズを180°から±30°方向ずらしてシュミレーションしていきます。（説明の為に、大きく30°ずらしてみます。）

先ずは、裸眼の状態での見え方です。

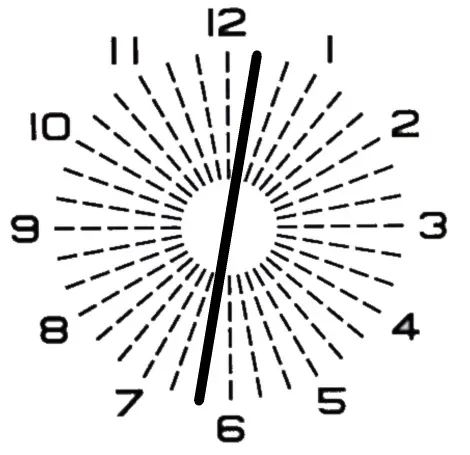
◎　『S−0.50 C−1.00 Ax10°』に、誤った乱視軸の『C−1.00 Ax180°』が装用されている状態の見え方です。

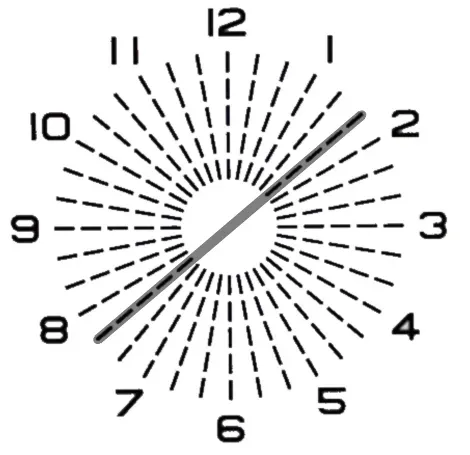
乱視度数が合っている場合、濃い線の方向が時計回り40°ずれた時点で、本来の乱視軸が半時計回りに10°ずれているという事がわかります。

(45°−40°)×２=10°だからなのですが、元々の補正軸と、誤りの補正軸の中間から45°逆方向にずれた角度に残余乱視が発生するからです。

何故、45°になるのかというのは、乱視度数は、縦軸を度数とし横軸を角度としたsinカーブを描き、眼の乱視要素と補正する乱視度数の合成レンズとなるからです。

◎　『S−0.50 C−1.00 Ax10°』に180°から30°回転させた『C−1.00 Ax30°』が装用されている状態の見え方です。計算上ではC−0.68DのAx155°方向に乱視の未補正があります。

軸度が155°になる理由は、10°と180°の中間5°から時計回りに45°の位置となるからです。

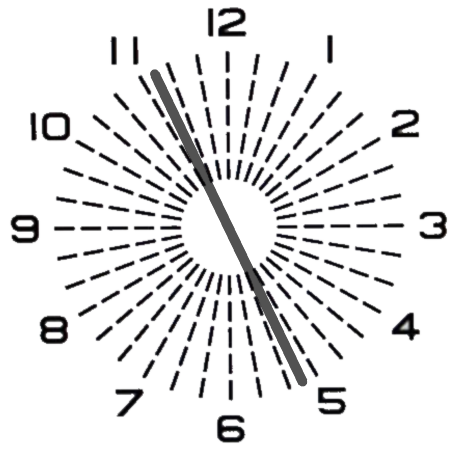
◎　『S−0.50 C−1.00 Ax10°』に180°から−30°回転させた『C−1.00 Ax150°』が装用されている状態の見え方です。計算上ではC−1.29DのAx35°方向に乱視の未補正があります。

軸度が35°になる理由は、10°と150°の中間170°から反時計回りに45°の位置となるからです。

◎　クロスシリンダー法による乱視測定での、1番と2番でハッキリ濃く見える方に修正していくのと同じ考え方となります。

因みに、乱視度数と軸方向のどちらも合っている場合、円柱軸を±30°ずらしても、同じ乱視の強さで逆方向に30°の残余乱視がそれぞれ発生します。

何故ならば、sin30°=1/2だからであり、度数は合成ですのでsin30°+sin30°=１となるからです。