乱視補正と残余乱視

Last Updated on 3年 by 管理者

『正乱視の補正』を考えてみましょう。

• 正乱視・・眼球の経線により屈折率の異なる乱視
  • 円柱レンズで矯正される
• 不正乱視・・主に角膜（まれに水晶体）の表面が凹凸不正の乱視
  • 基本的には眼鏡レンズで矯正されず、コンタクトレンズで矯正される
  • 角膜疾患により起こる事が多い
  • Placido角膜計で検査すると、同心円が不規則に歪んで見える

円錐角膜や翼状片などでは、『不正乱視』が多くみられます。

『不正乱視』の眼鏡補正はかなり複雑だと考えます。

詳しく説明しませんが、乱視処方をしない事では無く、不正乱視以外を補正していきます。

『進行などにより、度数変化が起こる』、『乱視度数の測定値が、本来よりも強く測定されやすい』という特徴があります。

正乱視の補正

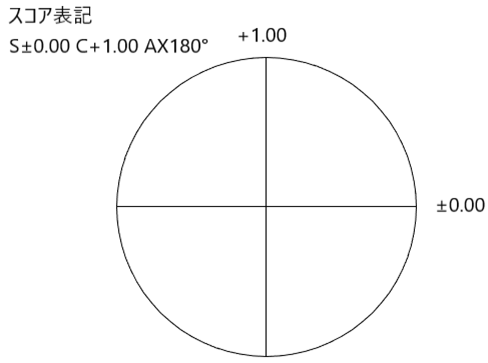
例えば、眼鏡レンズ『C−1.00 Ax180°』で補正される近視眼を考えますと、

眼の要素は『C+1.00 Ax180°』となります。

眼の要素が凸であり、凹レンズで相殺する事で補正できます。

スコア表記しますと、以下のようになります。

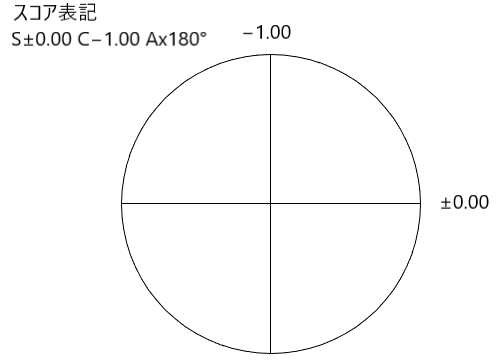
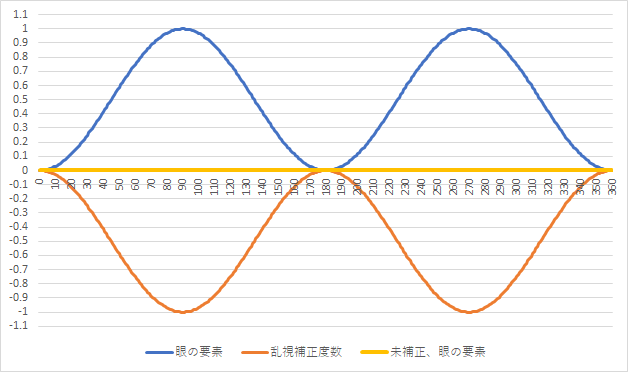
そして、円柱レンズは、『縦軸に屈折力[D]、横軸に方向[°]』として作図をしますと、以下の様なカーブとなります。

では、眼の要素『C+1.00 Ax180』の近視眼に、眼鏡レンズ『C−0.75 Ax180°』を装用させた場合の未補正度数はどうなるのでしょうか。

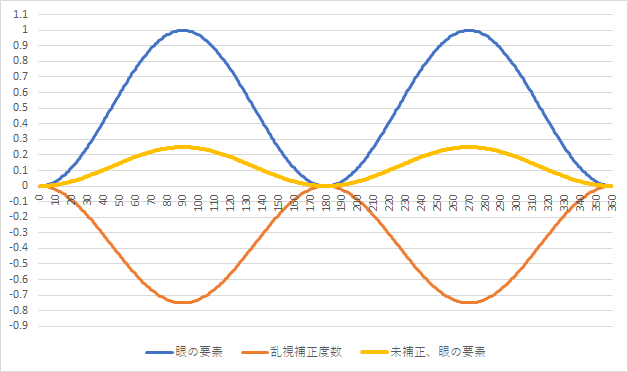
上図から、未補正度数は『C−0.25 Ax180』となるのがわかります。

因みに、眼の要素『C+1.00 Ax180°』の近視眼に、眼鏡レンズ『C−1.00 Ax10°』を装用させた場合の未補正度数は以下のようになります。

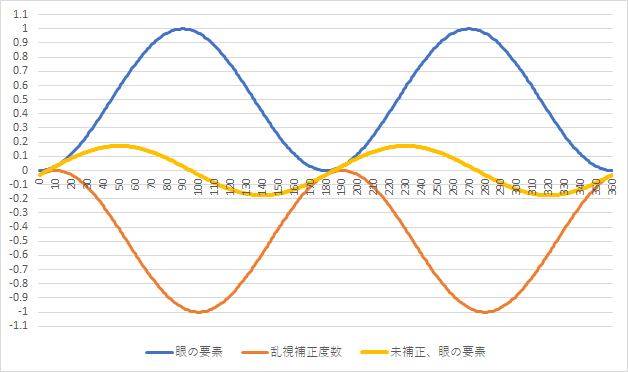
上図から、未補正度数は『C−0.35 Ax140°』となります。

完全補正と同じ乱視度数でも、

補正する乱視軸が10°ズレると、本来の乱視軸180と10°の半分の値から、45°ズレた方向に『別の乱視』が発生します。

この乱視を『残余乱視』といいます。

【上のような『残余乱視』を計算できるものを作成しました。】

このように正乱視は補正されています。