度付き水中眼鏡のレンズ形状

Last Updated on 2年 by 管理者

水中での度数

裸眼で水中に潜ると、角膜前面が大気中（屈折率1.0とする）ではなく水（屈折率3/4）に接します。

そうしますと、角膜の屈折力が殆ど零（角膜屈折力−0.29D）に等しくなります。

眼全体でみますと、水晶体の屈折力（屈折力+19.11D）のみが残ります。

結果として、猛烈な遠視状態（屈折力+18.8D）となります。

スネルの法則での、媒質１の屈折率n₁が、大気中（n_空気=1.00）から水中（n_水中=1.33）に変わるからです。

媒質２とは角膜を指します。そして、媒質３となる房水（ｎ_房水=1.336）へと達します。

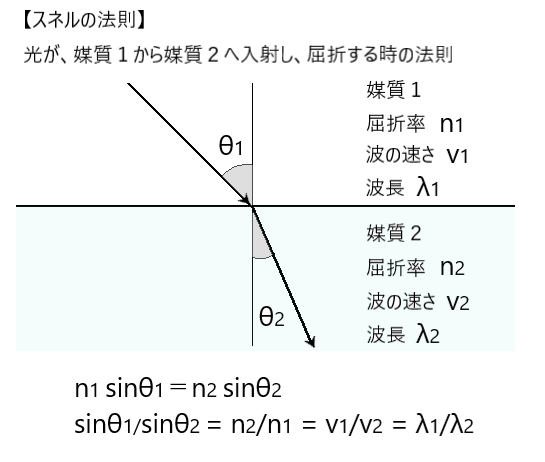
つまり、レンズ両側の媒質が異なる場合には、像側焦点距離 f’ と物側焦点距離 f は等しくなりません。

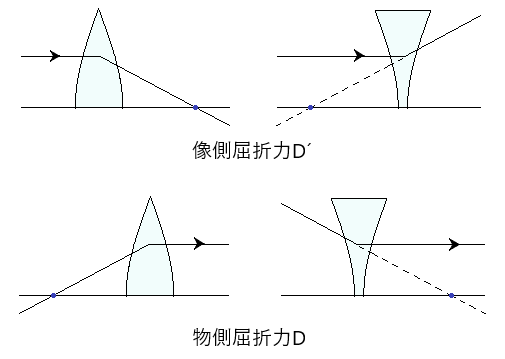
像側屈折力D’と物側屈折力Dも等しくはなりません。

模型眼

眼を1つの光学機器と考え、各部位の計測測定値を示す為に作成された眼球を『模型眼』といいます。

よく利用される『Gullstrand（グルストランド）の模型眼』では、角膜の前面屈折力は48.83Dであり、後面屈折力は−5.88Dです。

無調節時の水晶体屈折力は19.11Dであり、最大調節時の屈折力は33.06Dです。

無調節時の全屈折力は58.64Dであり、最大調節時では70.57Dとなります。

水中眼鏡の形状

像側頂点屈折力をD’_Vとしますと、

『D’_V＝ｎ/(ｎ/D’₁ -t)+D’₂』という関係が成り立ちます。

ｔ[mm]はレンズの厚みとし、D’₁はレンズ前面の像側屈折力、D’₂はレンズ後面の像側屈折力とします。

水中では、レンズ前面は水に接し、レンズ後面は空気に接しているものとします。

では、どういうレンズ形状が製作し易いのでしょうか。

薄レンズでは厚みｔが無視できますが、厚レンズの場合には無視できなくなります。

眼鏡レンズに近い『メニスカスレンズ』ではどうなのでしょうか。『凸平レンズ』や『平凸レンズ』ではどうなのでしょうか。

答えは『平凸レンズ』なのですが、何故そうなるのでしょうか。

それぞれ、一緒に計算しながら考察していきましょう。

メニスカスレンズ(眼鏡に近い形状)の場合

例として、S+4.00[D]の眼鏡で補正される遠視眼を考えます。

レンズの屈折率を1.5とし、
レンズ後面の像側屈折力 D’₂＝ −6.00[D]、
レンズ厚ｔ=10[ｍｍ]とします。

先ずは、水中での 像側頂点屈折力がD’_V水中=+4.00 [D]になる為の水中での像側前面屈折力はD’_1水中を求めます。

D’_V＝ｎ/(ｎ/D’₁ -t)+D’₂ の公式から

+4.00=1.5/(1.5/ D’_1水中 −0.001)+(−6.00)を計算しますと、
D’_1水中 ≒−4.11[D]となります。

これを、大気中での屈折力に換算する為に、

D’_1空気 ＝(n_レンズ−n_水)/r₁　から r₁ を求めますと、
r₁≒−0.041[ｍ]となります。

空気中での 像側前面屈折力D’_1空気 を求めますと、
D’_1空気 ＝(n_レンズ−n_空気)/r₁ ≒−12.20[D]となります。

像側頂点屈折力D’_V空気 ＝ ｎ_レンズ/(ｎ_レンズ/D’_1空気 -t)+D’₂ を計算しますと、
D’_V空気≒−17.28[D]となります。

レンズの厚みを無視した場合 のD’_V空気は約+23.9[D]となり、−17.28[D]と比べますと、差が大きいです。

メニスカスレンズで度付き水中眼鏡を作製しようとしますと、レンズの厚みｔによりレンズ前面屈折力 D’₁ が変わりますので、計算がとても面倒になります。

では、レンズの前面か後面を平らにした場合はどうでしょうか。

凸平レンズの場合

水中レンズの前面に凸平を付ける場合には、レンズ後面の D’₂ =0.00になります。

D’_V =+4.00[D]ですので、レンズ前面屈折力 D’₁ を求めるだけで良くなります。

+4.00=1.5/(1.5/ D’₁ −0.001)+0.00から
D’_1水中 =+3.90[D]となります。

メニスカスの計算と同様に・・・計算し、
r₁≒−0.043[ｍ] から D’_1空気 ≒11.63[D]となります。

D’_V空気≒+12.61[D] となります。

レンズの厚みを無視した場合 のD’_V空気は約+12.0[D]となり、+12.61[D]と比べますと、厚みによる誤差は少ないです。

平凸レンズの場合

水中レンズの後面に平凸を付ける場合には、レンズ前面の D’₁ =0.00になります。

+4.00=1.5/(1.5/ D’₁ −0.001)+ D’₂ から計算するのですが、
右辺の1.5/(1.5/ D’₁−0.001)＝1.5/(inf−0.001)＝1.5/inf＝0 となりますので、
D’₂ =+4.00[D]となります。

レンズの厚みに関係なく、レンズ後面の屈折力 D’₂のみを考えれば、必要なレンズを作製する事ができます。